Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
1986 Übersicht
nach oben
Aufgabe 1a:
Die Firma Meier stellt Zelte her. Der Grundtyp ist ein Zelt in der Form eines quadratischen Pyramidenstumpfes mit aufgesetzter quadratischer Pyramide. Es besteht aus einem innenliegenden Rohrgerüst, über das die vernähten Seitenflächen und Dachflächen gespannt werden.
Das Zelt hat folgende Maße (siehe nebenstehende Schrägbildskizze):
 
Berechnen Sie die Bodenfläche des Zeltes in Quadratmetern.
Berechnen Sie die Höhe 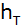des trapezförmigen Seitenteiles.
Wieviel Stoff benötigt man bei der Herstellung der vier Seitenwände, wenn für die Überlappungen mit 13% Zuschlag gerechnet wird?
4 P
Aufgabe 1b:
Die nebenstehende Skizze zeigt einen Schnitt des Zeltes parallel zu einer Grundkante. 
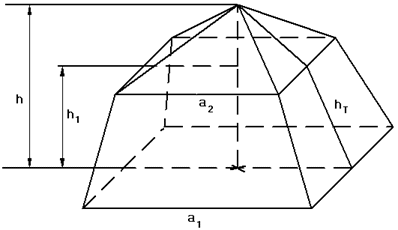
Berechnen Sie den Winkel 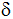an der Traufkante und den Rauminhalt des Zeltes.
  4 P
Aufgabe 1c:
Die Firma Meier stellt diesen Zelttyp auch mit folgenden anderen Maßen her: 
   
 
Höhen der Seitenflächen und Höhen der Dachflächen (siehe nebenstehenden Schnitt parallel zu einer Grundkante) betragen jeweils .
Berechnen Sie die Grundkante und die Deckkante sowie die Gesamtfläche der vier Seitenteile und vier Dachteile in Abhängigkeit von e.
Für welchen Wert von e ist zur Herstellung dieses Zeltes eine Stofffläche von 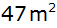(Verschnitt bleibt unberücksichtigt) notwendig?
  3 P
Aufgabe 2a:
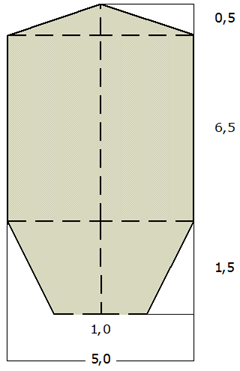
Ein Blechverarbeitungsbetrieb stellt einen runden, unten offenen Silobehälter her (siehe Skizze).
Wie viele Quadratmeter Blech sind dabei verarbeitet worden, wenn mit einer Verarbeitungszugabe von 5% gerechnet wurde?
(Alle Maße sind in Metern angegeben.)
4 P
Aufgabe 2b:
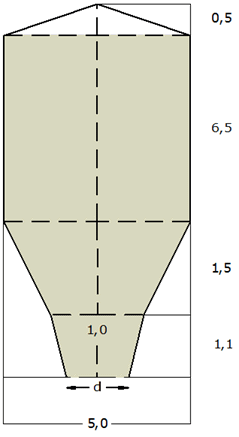
Welches Fassungsvermögen hat das Silo ohne den kegelförmigen Dachraum (siehe Skizze Aufgabe 2a)?
Die untere Öffnung des Silos wird mit einem Auslaßstutzen versehen (siehe Skizze).
Der Stutzen ist 1,1 m hoch und erhöht das Fassungsvermögen des Silos um 0,4 m3.
Berechnen Sie den unteren Durchmesser d des Stutzens. (Alle Maße sind in Metern angegeben.)
4 P
Aufgabe 2c:
Die nebenstehende Skizze zeigt den unteren Teil eines weiteren Silos.
Finden Sie eine Formel für das Fassungsvermögen dieses Teiles in Abhängigkeit von a und .
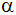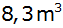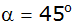Welche Durchmesser ergeben sich daraus für ein Fassungsvermögen von , wenn für den Winkel gewählt wird?
3 P
Aufgabe 3a:
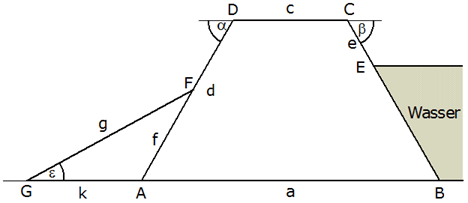
Der Querschnitt eines Flußdammes hat die Form eines Trapezes ABCD.
Die folgenden Strecken und Winkel wurden gemessen:
 
Berechnen Sie die Höhe h des Dammes sowie die Breite der Dammsohle .
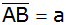Man mißt .
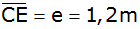Wie hoch steht das Wasser über ?
4 P
Aufgabe 3b:
Der Querschnitt eines Flußdammes hat die Form eines Trapezes ABCD.
Die folgenden Strecken und Winkel wurden gemessen:
 
   
Der Damm wird durch eine Aufschüttung GAF verstärkt.
Es sind:
  .
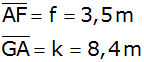Berechnen Sie die Querschnittsfläche GAF, die Länge der neuen Böschung 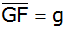und den Böschungswinkel .
4 P
Aufgabe 3c:
Der Querschnitt eines Flußdammes hat die Form eines Trapezes ABCD.
Die folgenden Strecken und Winkel wurden gemessen:
 
   
Der Damm wird durch eine Aufschüttung GAF verstärkt.
Es sind:
  .
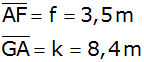Der Damm soll durch eine bis zum Punkt D reichende Aufschüttung verstärkt werden. 
Berechnen Sie 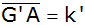in Abhängigkeit vom Böschungswinkel .
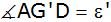Wie groß wird 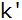  bei ?
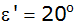  3 P
Aufgabe 4a:
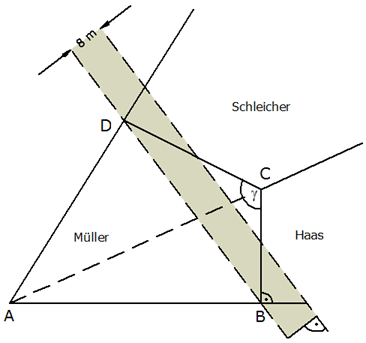
Der Bau einer neuen Sraße macht Grundstücksver- änderungen erforderlich. Die Straße ist 8 m breit und wird entlang einer Geraden BD geführt (siehe Skizze).
Folgende Werte werden gemessen:
Berechnen Sie den Flächeninhalt des Grundstückes ABCD von Landwirt Müller.
4 P
Aufgabe 4b:
Der Bau einer neuen Sraße macht Grundstücksver- änderungen erforderlich. Die Straße ist 8 m breit und wird entlang einer Geraden BD geführt (siehe Skizze).
Folgende Werte werden gemessen:
Berechnen Sie die Länge der neuen Grundstückgrenze BD sowie den Winkel, unter dem die Straße auf AB trifft.
Wie viele Quadratmeter verbleiben Landwirt Müller noch, wenn er die Fläche BCD abtreten muß?
4 P
Aufgabe 4c:
Der Bau einer neuen Sraße macht Grundstücksver- änderungen erforderlich. Die Straße ist 8 m breit und wird entlang einer Geraden BD geführt (siehe Skizze).
Folgende Werte werden gemessen:
Wie viele Quadratmeter gehen dem Landwirt Haas durch den Bau der Straße verloren, wenn der Winkel 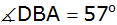beträgt?
 
3 P
Aufgabe 5a:
Der Kauf eines neuen Autos mit Katalysator bringt Steuervorteile (wie die Gegebüberstellung zeigt):
Auto mit Katalysator
  • zunächst 6 Jahre und 10 Monate steuerfrei
  • danach für je 100 cm3 Hubraum jährlich 13,20 DM Steuer
Auto ohne Katalysator
  • kostet für die ganze Zeit für je 100 cm3 Hubraum jährlich 21,60 DM Steuer
Herr Haller kauft ein Auto mit Katalysator, das 1500 cm3 Hubraum hat. Er will es 9 Jahre fahren.
Berechnen Sie die Steuerersparnis gegenüber dem Auto ohne Katalysator (in DM und in %).
4 P
Aufgabe 5b:
Zur Finanzierung des Autos fehlen Herrn Haller noch 3.800,00 DM. Er nimmt diese Summe als Kleinkredit auf.
Der Kleinkredit wird einschließlich der Kreditkosten in 24 Monaten zurückgezahlt.
Die Bank berechnet eine einmalige Bearbeitungsgebühr von 2% und einen monatlichen Zinssatz von 0,55%,
jeweils bezogen auf den vollen Kreditbetrag.
Sie rundet die monatlichen Rückzahlunsraten auf volle Markbeträge auf und zieht den zuviel bezahlten Betrag
von der letzten Rate ab.
Wie hoch ist jede der ersten 23 gleichen Raten, und wie hoch ist die letzte (24.) Rate?
4 P
Aufgabe 5c:
Herr Haller rechnet mit einer jährlichen Wertminderung seines Autos von 20%, jeweils bezogen auf den
Zeitwert des Vorjahres.
Stellen Sie den Zeitwert des Autos über 5 Jahre in einem geeigneten Koordinatensystem dar, wenn der
Neupreis 20.000,00 DM beträgt.
Nach welcher Zeit muß er seinen Wagen spätestens verkaufen, wenn er noch 7.000,00 DM erhalten will?
3 P
Aufgabe 6a:
In der Bundesrepublik Deutschland werden Luftverunreinigungen (Emissionen) durch Stickstoffoxide,
Schwefeldioxide und Staub ständig gemessen.
Luftverunreinigungen durch Stickstoffoxide
Im Jahre 1982: 3,1 Millionen Tonnen, verteilt auf Verkehr (54,6%), Haushalte (3,7%), Kraftwerke (27,7%)
und Industrie (14,0%).
Stellen Sie den prozentualen Anteil der Verursacher in einem geeigneten Schaubild dar.
Berechnen Sie die Anteile für Verkehr und Industrie (in Millionen Tonnen).
Der Anteil der Chemiewerke betrug 81.000 Tonnen.
Berechnen Sie den prozentualen Anteil der Chemiewerke am Industrieausstoß und am Gesamtausstoß.
4 P
Aufgabe 6b:
In der Bundesrepublik Deutschland werden Luftverunreinigungen (Emissionen) durch Stickstoffoxide,
Schwefeldioxide und Staub ständig gemessen.
Luftverunreinigungen durch Schwefeldioxid
Im Jahre 1982 entfielen auf: Verkehr 102.000 t, Haushalte 279.000 t, Kraftwerke 1.863.000 t
und Industrie 756.000 t.
Gesetzliche Auflagen zwingen die Kraftwerke, den Schwefeldioxidausstoß von 850 mg/m3 auf 400 mg/m3
Abluft zu verringern.
Berechnen Sie den prozentualen Anteil der Kraftwerke am Gesamtausstoß und die prozentuale Abnahme,
die zukünftig durch die gesetzlichen Auflagen bei Kraftwerken erzielt wird.
Wieviel Tausend Tonnen Schwefeldioxid hätten die Kraftwerke 1982 weniger ausgestoßen, wenn diese
gesetzlichen Auflagen schon damals in Kraft gewesen wären?
4 P
Aufgabe 6c:
In der Bundesrepublik Deutschland werden Luftverunreinigungen (Emissionen) durch Stickstoffoxide,
Schwefeldioxide und Staub ständig gemessen.
Luftverunreinigungen durch Staub
1954 betrug die Staub-Emission 6,4 Millionen Tonnen.
Seither konnte sie alle 8 Jahre um die Hälfte gesenkt werden.
Stellen Sie in einem Koordinatensystem den Verlauf der Staubemissionswerte dar, und entnehmen Sie
dem Graphen den voraussichtlichen Wert für 1990.
3 P