|
Aufgabe 1a: |
Das Dach eines
Turmes hat die Form einer quadratischen Pyramide. Es
ist
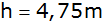 hoch.
hoch. |
Die Neigung der
Dachfläche beträgt
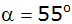 (siehe Skizze).
(siehe Skizze). |
|
Das Dach wird mit Kupferblech eingedeckt. Für
Verschnitt und Falz sind zusammen 15%
hinzuzurechnen. |
Berechnen Sie
die Grundkante a, die Höhe
 der Seitenfläche und den Verbrauch an Kupferblech.
der Seitenfläche und den Verbrauch an Kupferblech. |
|
|
 |
4 P |
|
|
Aufgabe 1b: |
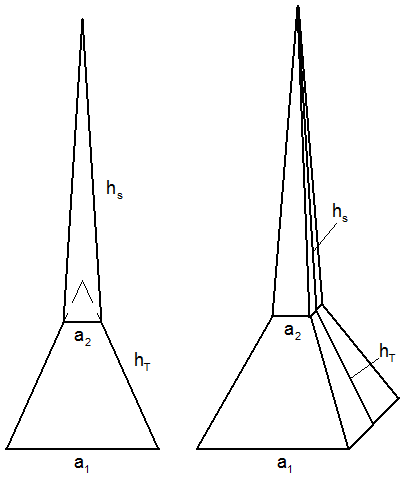
| Das Dach eines
anderen Turmes hatte ursprünglich ebenfalls die Form
einer quadratischen Pyramide. Es wurde durch
Aufsetzen einer spitzeren Pyramide erhöht, so daß es
jetzt die Form eines quadratischen Pyramidenstumpfes
mit aufgesetzter quadratischer Pyramide hat (siehe
Skizzen). |
Die Höhen der
Dachflächen sind
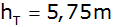 und
und
 ;
die gemeinsame Kante ;
die gemeinsame Kante
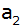 mißt
mißt
 . . |
Die Gesamtdachfläche ist
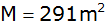 groß.
groß. |
Berechnen Sie
die Länge der Grundkante
 und die Höhe
und die Höhe
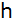 des ursprünglichen Daches.
des ursprünglichen Daches. |
|
|
 |
4 P |
|
|
Aufgabe 1c: |
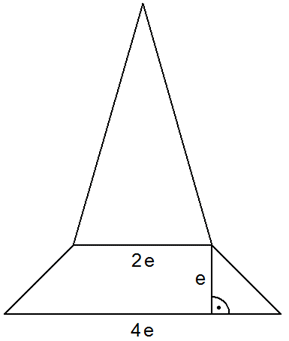
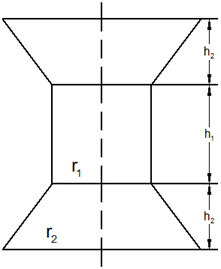
| Der
nebenstehende Achsenschnitt parallel zu einer
Grundkante zeigt ein entsprechendes Turmdach. Die
Mantelfläche des quadratischen Pyramidenstumpfes ist
flächengleich zur Mantelfläche der aufgesetzten
Pyramide. |
Zeigen Sie, daß
für die Gesamthöhe
 des Turmdaches gilt:
des Turmdaches gilt: |
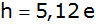 . . |
|
|
 |
3 P |
|
|
Aufgabe 2a: |
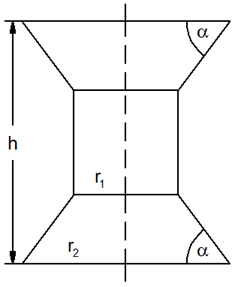
| Ein Werkstück
besteht aus einem Zylinder mit zwei aufgesetzten
gleich großen Kegelstümpfen (siehe Skizze). |
| Es hat folgende
Maße: |
|
|
|
Berechnen Sie die Oberfläche dieses Werkstückes. |
|
|
 |
4 P |
|
|
Aufgabe 2b: |
Ein anderes
Werkstück besitzt ein Volumen von
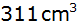 . . |
| Ferner sind
bekannt: |
|
|
|
(siehe Skizze). |
Berechnen Sie
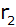 . . |
|
|
 |
4 P |
|
|
Aufgabe 2c: |
Eine
Aluminiumplatte von
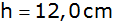 Dicke wird nach nebenstehender Skizze durchbohrt (
Dicke wird nach nebenstehender Skizze durchbohrt ( )
und ausgefräst ( )
und ausgefräst ( ). ). |
Zeigen Sie, daß
das Volumen des entstandenen Hohlraumes in
Abhängigkeit von
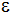 nach der Formel
nach der Formel
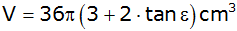 berechnet werden kann.
berechnet werden kann. |
|
|
 |
3 P |
|
|
Aufgabe 3a: |
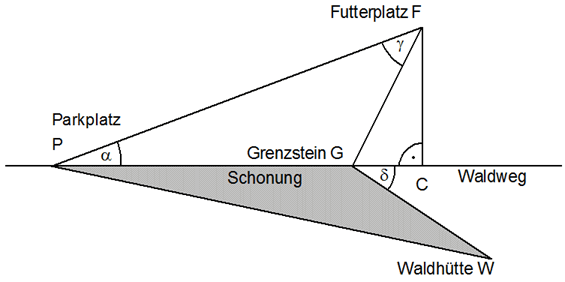
| Nebenstehende
Skizze zeigt einen Ausschnitt aus einem Waldstück. |
| Es sind
bekannt: |
|
|
| Berechnen Sie
(im Dreieck PGF) die Länge des Pfades vom Grenzstein
G zum Futterplatz F. |
| Welche
Entfernung hat Punkt C vom Grenzstein G und vom
Futterplatz F? |
|
|
 |
4 P |
|
|
Aufgabe 3b: |
| Nebenstehende
Skizze zeigt einen Ausschnitt aus einem Waldstück. |
| Es sind
bekannt: |
|
|
| Berechnen Sie
Umfang und Flächeninhalt der Schonung. |
|
|
 |
4 P |
|
|
Aufgabe 3c: |
| Nebenstehende
Skizze zeigt einen Ausschnitt aus einem Waldstück. |
| Es sind
bekannt: |
|
|
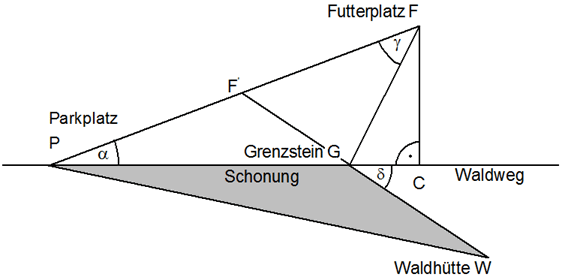
| Der Futterplatz
F wird in Richtung P so verlegt, daß er von W über G
direkt (geradlinig) erreichbar ist. |
| Um welche
Strecke verkürzt sich dadurch die Entfernung vom
Parkplatz zum Futterplatz? |
|
|
 |
3 P |
|
|
Aufgabe 4a: |
Herr M. besitzt
ein Grundstück in der Form eines Trapezes ABCD (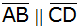 )
mit den Seiten )
mit den Seiten  und und 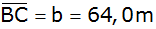 sowie den Winkeln sowie den Winkeln  und
und  . . |
| Zeichnen Sie
das Grundstück im Maßstab 1 : 1000 und berechnen Sie
seinen Flächeninhalt. |
|
|
4 P |
|
|
Aufgabe 4b: |
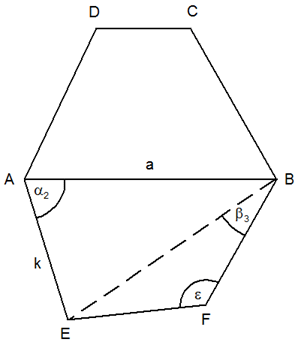
Herr M. kann
sein Grundstück um ein anderes erweitern, dessen
Maße
 , ,
 ,
und Winkel ,
und Winkel
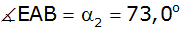 , ,
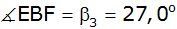 , ,
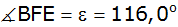 betragen (siehe Skizze).
betragen (siehe Skizze). |
| Welchen Betrag
muß Herr M. für das neue Grundstück AEFB bezahlen,
wenn der Quadratmeterpreis 40,00 DM beträgt? |
|
|
 |
4 P |
|
|
Aufgabe 4c: |
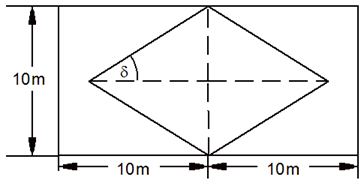
| Herr M.
pflastert in seinem Grundstück eine rechteckige
Fläche von 20 m Länge und 10 m Breite mit schwarzen
Steinen. Zur optischen Auflockerung wird im Inneren
des Rechteckes eine rautenförmige Fläche mit roten
Steinen verlegt (siehe Skizze). |
Der Winkel
 beträgt
beträgt
 .
Berechnen Sie die Kosten für das Pflaster, wenn der
Preis für die schwarzen Steine 40 DM pro
Quadratmeter und der für die roten Steine 60 DM pro
Quadratmeter beträgt. .
Berechnen Sie die Kosten für das Pflaster, wenn der
Preis für die schwarzen Steine 40 DM pro
Quadratmeter und der für die roten Steine 60 DM pro
Quadratmeter beträgt. |
Zeigen Sie, daß
zur Berechnung der Gesamtkosten in Abhängigkeit von
 die Formel
die Formel |
|
|
| verwendet
werden kann. |
|
|
 |
3 P |
|
|
Aufgabe
5a: |
| Günters
Leichtkraftrad benötigt ein Benzin-Öl-Gemisch.
Günter tankt 6 Liter Benzin und 0,25 Liter Öl. |
| Wieviel Prozent
Öl enthält das Gemisch? |
Berechnen Sie,
welche Strecke Günter mit dieser Tankfüllung fahren
kann, wenn 2,5 Liter Gemisch
auf einer Strecke
von 100 km verbraucht werden. |
| Wieviel Benzin
und wieviel Öl benötigt das Kleinkraftrad für eine
Strecke von 680 km? |
|
|
4 P |
|
|
Aufgabe
5b: |
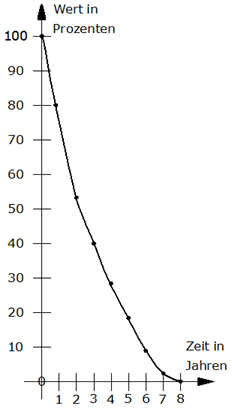
| Günters Leichtkraftrad kostet
neu 3.420 DM. Die Maschine verliert
jährlich an Wert. Nebenstehende
Grafik zeigt den Zeitwert in
Prozenten in Abhängigkeit von der
Anzahl der Jahre (bei einem Neupreis
von 100%). |
| Ermitteln Sie den Zeitwertbetrag
des Kleinkraftrades nach 5 Jahren. |
| Günter fährt im Jahr
durchschnittlich 2.300 km. |
| An Kosten entstehen: |
| |
- 2,4 l Benzin auf 100
km Strecke zu 1,34 DM je
Liter
- 0,1 l Öl auf 100 km
Strecke zu 4,60 DM je
Liter
- Versicherungskosten
450 DM pro Jahr
- Nebenkosten
(Reparaturen, Bereifung,
TÜV-Gebühren und
ähnliche Ausgaben)
insgesamt 85 DM pro
Jahr.
|
|
| Berechnen Sie die Gesamtkosten
(einschließlich Wertminderung) für
die ersten 5 Jahre und daraus die
durchschnittlichen Kosten für einen
gefahrenen Kilometer. |
|
 |
|
|
|
4 P |
|
|
Aufgabe
5c: |
Berechnen Sie die
durchschnittlichen Kosten für einen
gefahrenen Kilometer über einen
Zeitraum von 8 Jahren,
wenn in
den letzten beiden Jahren der
Benzinpreis um 5% und der Ölpreis um
12% über dem entsprechenden
Preis
der ersten 6 Jahre lag. |
| (Für die Berechnung gelten die
in Aufgabe 5b genannten Werte.) |
|
|
|
|
3 P |
|
|
Aufgabe 6a: |
|
In der folgenden Tabelle sind monatliche Ausgaben eines
4-Personen Haushaltes für die Jahre 1980 und 1984
aufgeführt: |
 |
|
|
Berechnen Sie für das Jahr 1980 den prozentualen Anteil der
einzelnen Ausgabeposten an den Gesamtkosten
und stellen
Sie diese in einem Diagramm dar. |
|
Wie hoch ist der prozentuale Anstieg der Gesamtkosten von
1980 bis 1984? |
|
4 P |
|
|
Aufgabe 6b: |
|
In der folgenden Tabelle sind monatliche Ausgaben eines
4-Personen Haushaltes für die Jahre 1980 und 1984
aufgeführt: |
 |
|
|
|
Für die weiteren Zeiträume 1984 - 1988, 1988 - 1992, 1992 -
1996 bleiben die Wachstumsraten der Bereiche "Nahrung" und
"Wohnung" die gleichen wie für den Zeitraum 1980 - 1984. |
|
Berechnen Sie die jeweilige Wachstumsrate der Ausgaben für
"Nahrung" und "Wohnung". |
Zeichnen Sie in ein Koordinatensystem (Abszisse:
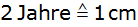 ;
Ordinate: ;
Ordinate:
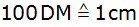 ) den
erwarteten Entwicklungsverlauf der Ausgaben für "Nahrung"
und "Wohnung". ) den
erwarteten Entwicklungsverlauf der Ausgaben für "Nahrung"
und "Wohnung". |
|
Entnehmen Sie der Zeichnung den Zeitpunkt, an dem die
Ausgaben für "Nahrung" und "Wohnung" gleich hoch sind. |
|
4 P |
|
|
Aufgabe 6c: |
|
Die Einkünfte und die Ausgaben des Jahres 1981 werden mit
dem Grundwert 100% angesetzt, um die Entwicklung für die
folgenden Jahre damit vergleichen zu können. |
|
Dabei ergaben sich jeweils im Vergleich zum Vorjahr folgende
prozentuale Wachstumsraten: |
|
|
|
|
|
Um wieviel Prozent sind die Einkünfte und die Ausgaben von
1981 bis 1984 jeweils gestiegen? |
|
Um eine Prognose der Ausgaben für das Jahr 2000 aufstellen
zu können, wird ab 1985 von einer jährlichen Wachstumsrate
von 3% ausgegangen. |
|
Mit welchen monatlichen Gesamtausgaben kann damit im Jahr
2000 gerechnet werden, wenn 1984 diese 2650 DM betrugen? |
|
3 P |
|
|
|
|
|