|
Aufgabe 1a: |
Eine
quadratische Pyramide ist durch die Seitenkante
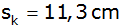 und den Neigungswinkel
und den Neigungswinkel
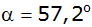 zwischen der Seitenkante und der Grundfläche
bestimmt.
zwischen der Seitenkante und der Grundfläche
bestimmt. |
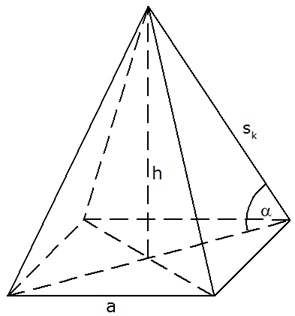
| Berechnen Sie
die Höhe h, die Grundkante a und das Volumen V
dieser Pyramide. |
|
|
 |
4 P |
|
|
Aufgabe 1b: |
Einem
quadratischen Pyramidenstumpf mit der Grundkante 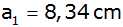 und der Höhe
und der Höhe  wird seine Ergänzungspyramide
aufgesetzt. Diese hat die Höhe wird seine Ergänzungspyramide
aufgesetzt. Diese hat die Höhe
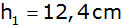 . . |
| Fertigen Sie
eine Schrägbildskizze an und kennzeichnen Sie die
gegebenen Größen. |
Berechnen Sie
die Deckkante  und die Mantelfläche des
Pyramidenstumpfes. und die Mantelfläche des
Pyramidenstumpfes. |
|
|
4 P |
|
|
Aufgabe 1c: |
Gegeben ist
eine quadratische Pyramide mit der Grundkante
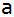 .
Der Neigungswinkel zwischen der Seiten- .
Der Neigungswinkel zwischen der Seiten-
kante und
der Grundfläche ist
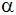 . . |
Zeigen Sie, daß
sich das Volumen der Pyramide mit der Formel
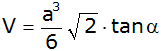 berechnen läßt.
berechnen läßt. |
Für welchen
Winkel
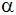 hat diese Pyramide das gleiche Volumen wie ein
Würfel mit der Kantenlänge
hat diese Pyramide das gleiche Volumen wie ein
Würfel mit der Kantenlänge
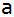 ? ? |
|
|
3 P |
|
|
Aufgabe 2a: |
In einem
rechtwinkligen Koordinatensystem (Längeneinheit 1
cm) ist das Dreieck ABC durch die Koordinaten
seiner Eckpunkte
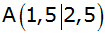 , ,
 und
und
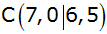 gegeben.
gegeben. |
| Zeichnen Sie
dieses Dreieck und berechnen Sie seine Seitenlängen. |
| Das Dreieck
rotiert um die x-Achse. |
| Berechnen Sie
die Oberfläche des entstehenden Rotationskörpers. |
|
|
4 P |
|
|
Aufgabe 2b: |
Ein Kegelstumpf
ist durch das Volumen
 ,
die Deckkreisfläche ,
die Deckkreisfläche
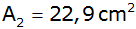 und die
und die
Höhe
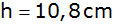 gegeben.
gegeben. |
| Berechnen Sie
die Oberfläche des Kegelstumpfes. |
|
|
4 P |
|
|
Aufgabe 2c: |
Ein Trinkglas
hat die Form eines Kegels mit dem Öffnungswinkel
 . . |
Geben Sie einen
Term für das Wasservolumen in Abhängigkeit von der
Glashöhe
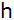 an.
an. |
In welcher
Entfernung
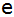 von der Kegelspitze aus muß die Markierung für ein
Volumen von 0,2 Liter am
von der Kegelspitze aus muß die Markierung für ein
Volumen von 0,2 Liter am
Glas angebracht werden? |
|
|
3 P |
|
|
Aufgabe 3a: |
Ein in A und D
rechtwinkliges Trapez ABCD hat die Seiten
 , ,

und den Winkel
 . . |
Berechnen Sie
die Seiten
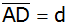 , ,
 ,
den Winkel ,
den Winkel
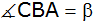 und die Fläche
und die Fläche
 dieses Trapezes.
dieses Trapezes. |
|
|
4 P |
|
|
Aufgabe 3b: |
Von
einem Trapez ABCD sind die Seiten
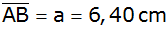 und
und
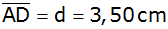 sowie die Winkel
sowie die Winkel
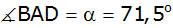 und
und
 gegeben.
gegeben. |
|
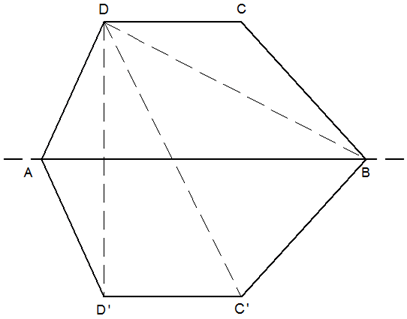
Dieses Trapez wird an AB gespiegelt (siehe Skizze). |
Berechnen Sie die Längen der Strecken
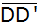 , ,
 und
und
 . . |
|
|
 |
4 P |
|
|
Aufgabe 3c: |
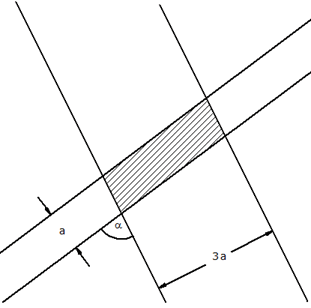
| Zwei
Papierstreifen mit den Breiten a und 3a überdecken
sich (siehe Skizze). |
Stellen Sie eine Formel für den Flächeninhalt der
gestrichelten Überdeckungsfigur in Abhängigkeit von
a und
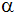 auf.
auf. |
Für welchen Wert von
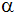 ist der Flächeninhalt der Überdeckungs- figur am
kleinsten? Begründen Sie Ihre Aussage mit Hilfe der
Formel.
ist der Flächeninhalt der Überdeckungs- figur am
kleinsten? Begründen Sie Ihre Aussage mit Hilfe der
Formel. |
|
|
 |
3 P |
|
|
Aufgabe 4a: |
Ein Drachen
ABCD hat die Symmetrieachse AC. Vom Drachen sind die
Längen der beiden Diagonalen
 und
und
 sowie der Winkel
sowie der Winkel
 bekannt.
bekannt. |
Berechnen Sie
den Umfang des Drachens und den Winkel
 . . |
|
|
4 P |
|
|
Aufgabe 4b: |
Ein
Parallelogramm ABCD hat die Seitenlängen
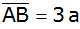 und
und
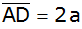 sowie den Winkel
sowie den Winkel
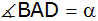 . . |
Zeigen Sie, daß
der Flächeninhalt dieses Parallelogramms nach der
Formel
 zu berechnen ist.
zu berechnen ist. |
Tabellieren Sie
die Werte für den Flächeninhalt in Abhängigkeit von
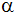 in Schritten von
in Schritten von
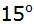 im Intervall
im Intervall
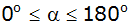 für
für
 . . |
| Stellen Sie
diese Abhängigkeit in einem rechtwinkligen
Koordinatensystem graphisch dar. |
(Abszisse:
Winkel
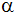 : :
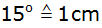 ;
Ordinate: Fläche ;
Ordinate: Fläche
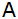 : :
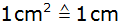 .) .) |
Entnehmen Sie
der Zeichnung, für welche Werte von
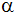 der Flächeninhalt
der Flächeninhalt
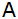 den Wert
den Wert
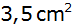 annimmt.
annimmt. |
| Kennzeichnen
Sie diese Werte. |
Bei welchem
Wert von
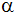 ist der Flächeninhalt
ist der Flächeninhalt
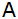 am größten?
am größten? |
| Wie heißt dann
die Figur? |
|
|
4 P |
|
|
Aufgabe 4c: |
Im
nebenstehenden Kreisausschnitt MAB soll der
Flächeninhalt
 der schraffierten Fläche in Abhängigkeit von
der schraffierten Fläche in Abhängigkeit von
 berechnet werden.
berechnet werden. |
| Es gilt: |
| |
 . . |
|
Zeigen Sie, daß
für den Flächeninhalt die Formel
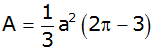 gilt.
gilt. |
Für welchen
Wert von a beträgt der Flächeninhalt
 ? ? |
|
|
 |
3 P |
|
|
Aufgabe 5a: |
| 1. |
Die Gleichung
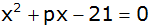 hat die
Lösungen hat die
Lösungen  und
und  ,
von denen die erste ,
von denen die erste
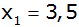 lautet. lautet. |
| |
Berechnen Sie
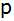 und
und  . . |
| 2. |
Bestimmen Sie die Definitionsmenge
und die Lösungsmenge der folgenden Gleichung: |
| |
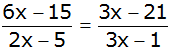 |
| |
|
|
4 P |
|
|
Aufgabe 5b: |
| 1. |
Für welche Werte von k hat die
Gleichung
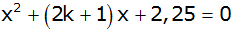 nur
eine (zusammenfallende) reelle Lösung? nur
eine (zusammenfallende) reelle Lösung? |
| |
Geben Sie die entsprechenden
Gleichungen an. |
| 2. |
Zwei Seiten eines Dreieckes
unterscheiden sich um 1,5 cm. Die dritte Seite ist 3 cm
länger als die kürzeste Seite. |
| |
Für welche Seitenlängen ist das
Dreieck rechtwinklig? |
|
|
4 P |
|
|
Aufgabe 5c: |
| Frau Huber bezahlt an einer
Autobahntankstelle 63 DM für Benzin. An der Tankstelle zu
Hause hätte sie für denselben Betrag 3 Liter Benzin mehr
erhalten, da es dort um 10 Pfennige je Liter billiger ist. |
| Wieviel kostete 1 Liter Benzin an
der Autobahntankstelle und wie viele Liter Benzin hat Frau
Huber dort getankt? |
|
|
3 P |
|
|
Aufgabe 6a: |
| Herr Gerhard möchte ein Motorrad
kaufen. Daher prüft er die Angebote zweier Händler. |
| Händler Amann bietet das Motorrad
für 4.200 DM zuzüglich 14% Mehrwertsteuer an. Er gewährt
2,5% Skonto. |
| Händler Berger verlangt 4.800 DM
einschließlich der Mehrwertsteuer von 14%; außerdem noch 109
DM Überführungskosten. Auf den Gesamtpreis gewährt er 3%
Skonto. |
| Welches Angebot der beiden Händler
ist günstiger? |
| Um wieviel Prozent liegt das
ungünstigere Angebot über dem günstigeren Angebot? |
|
|
4 P |
|
|
Aufgabe 6b: |
Herr Gerhard kauft das Motorrad und
gleichzeitig einen Helm für zusammen 4.800 DM. Er hat schon
vor
4 Jahren 2.500 DM auf einen Sparvertrag eingezahlt.
Die Bank zahlte in diesen 4 Jahren 5%, 5%, 6%, 6%
Zinsen
sowie nach Ablauf dieser 4 Jahre 12% der Zinsen als
Sparzulage. |
Welchen Betrag hat Herr Gerhard
angespart, wenn die Zinsen jeweils dem Vertrag
gutgeschrieben und mitver-
zinst wurden? |
| Um die Rechnung vollständig
begleichen zu können, überzieht Herr Gerhard sein Girokonto
um den Differenz- betrag aus Rechnungssumme und
Vertragsguthaben für 24 Tage. Der Zinssatz für die
Kontoüberziehung beträgt 13%. |
| Wie hoch sind die
Überziehungszinsen? |
|
|
4 P |
|
|
Aufgabe 6c: |
| Herr Gerhard macht mit seinem
Motorrad eine Bodenseerundfahrt. Er wechselt daher Deutsche
Mark (DM) in Österreichische Schillinge und Schweizer
Franken zu folgenden Kursen um: |
| 1 Schweizer Franken kostet 1,24 DM
und 10 Österreichische Schillinge kosten 1,40 DM. |
| Er wechselt 312 DM und erhält
sechsmal so viele Schillinge wie Franken. |
| Wie viele Schillinge und Franken
erhält Herr Gerhard? |
| Nach der Reise hat Herr Gerhard noch
40 Schweizer Franken übrig, dafür zahlt ihm die Bank 48,40
DM. |
| Um wieviel Prozent ist der Kurs beim
Zurückwechseln ungünstiger? |
|
|
3 P |
|