|
Aufgabe 1a: |
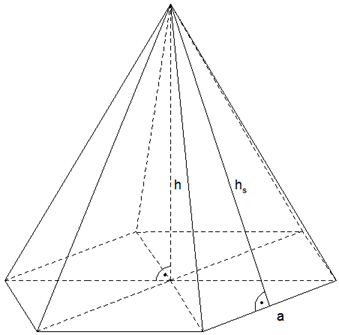
Eine
regelmäßige sechsseitige Pyramide ist durch ihre
Mantelfläche
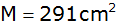 und ihre Seitenflächenhöhe
und ihre Seitenflächenhöhe
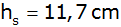 gegeben.
gegeben. |
| Berechnen Sie
die Grundkante a, die Körperhöhe h und die
Oberfläche O dieser Pyramide. |
|
|
 |
4 P |
|
|
Aufgabe 1b: |
| Die
Seitenfläche eines regelmäßigen sechsseitigen
Pyramidenstumpfes ist das gleichschenklige Trapez
ABCD. |
Es gilt
 , ,
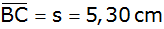 und
und
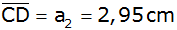 . . |
Berechnen Sie
die Höhe
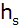 der Seitenfläche sowie die Mantellfläche M und die
Körperhöhe h dieses Pyramidenstumpfes.
der Seitenfläche sowie die Mantellfläche M und die
Körperhöhe h dieses Pyramidenstumpfes. |
|
|
4 P |
|
|
Aufgabe 1c: |
Bei einem
regelmäßigen sechsseitigen Prisma ist die Maßzahl
der Grundkante a gleich der Maßzahl der Körper-
höhe h. Das Prismavolumen beträgt
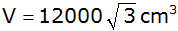 . . |
Zeigen Sie, daß
dann die Kantenlänge
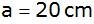 und die Oberfläche
und die Oberfläche
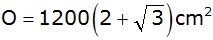 betragen.
betragen. |
|
|
3 P |
|
|
Aufgabe 2a: |
| Die
nebenstehende schraffierte Fläche rotiert um die
angegebene Achse R. Dadurch entsteht ein
Rotationskörper. |
Berechnen Sie
die Strecke s sowie die Oberfläche O und das Volumen
V dieses Rotationskörpers mit
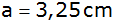 . . |
|
|
 |
4 P |
|
|
Aufgabe 2b: |
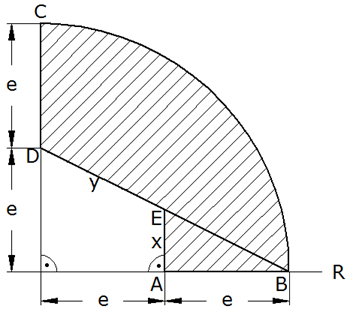
| Die
nebenstehende schraffierte Fläche rotiert um die
angegebene Achse R. Dadurch entsteht ein
Rotationskörper. |
Berechnen Sie
für
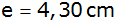 die Strecken
die Strecken
 und
und
 sowie die Oberfläche O dieses Rotationskörpers.
sowie die Oberfläche O dieses Rotationskörpers. |
|
|
 |
4 P |
|
|
Aufgabe 2c: |
| Die
nebenstehende schraffierte Fläche rotiert um die
angegebene Achse R. Dadurch entsteht ein
Rotationskörper. |
Geben Sie das
Volumen V und die Oberfläche O dieses
Rotationskörpers in Abhängigkeit von c als
Vielfaches von
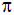 an.
an. |
| Für welchen
Wert von c haben V und O des Rotationskörpers die
gleiche Maßzahl? |
|
|
 |
3 P |
|
|
Aufgabe 3a: |
Von einem
Viereck ABCD sind die Seiten
 und
und
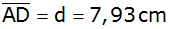 sowie die Winkel
sowie die Winkel
 , ,
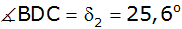 und
und
 gegeben.
gegeben. |
Berechnen Sie
sowohl die Seiten
 und
und
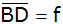 als auch die Winkel
als auch die Winkel
 und
und
 . . |
|
|
 |
4 P |
|
|
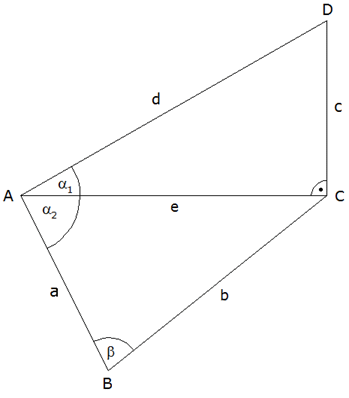
Aufgabe 3b: |
Von einem
Viereck ABCD sind die Winkel
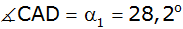 , ,
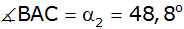 , ,
 und
und
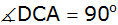 sowie die Diagonale
sowie die Diagonale
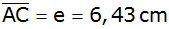 gegeben.
gegeben. |
Berechnen Sie
die Seiten
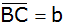 und
und
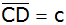 sowie den Umfang u des Teildreieckes BCD.
sowie den Umfang u des Teildreieckes BCD. |
|
|
 |
4 P |
|
|
Aufgabe 3c: |
| In
nebenstehender Figur soll der Flächeninhalt der
schraffierten Fläche in Abhängigkeit von a berechnet
werden. |
Es ist
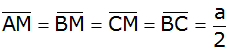 . . |
| Zeigen Sie,daß
für den Flächeninhalt gilt: |
| |
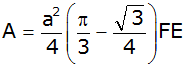 . . |
|
Welchen Wert
nimmt a für
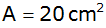 an?
an? |
|
|
 |
3 P |
|
|
Aufgabe 4a: |
| 1. |
Bestimmen Sie graphisch mit Hilfe des
Einheitskreises (1 LE = 5 cm) die Lösungen
der Aussageform
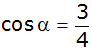 im Intervall
im Intervall
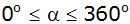 . . |
|
|
2. |
Zeigen Sie mit Hilfe
einer geeigneten Figur, daß
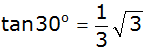 ist.
ist. |
|
|
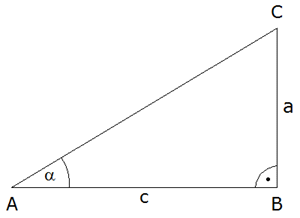
3. |
Im nebenstehenden
Dreieck ABC ist
 . .
Berechnen Sie, um
welche Strecke a' die Seite
 über C hinaus verlängert werden muß, damit
der Winkel
über C hinaus verlängert werden muß, damit
der Winkel
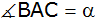 verdoppelt wird.
verdoppelt wird. |
 |
|
|
|
|
|
|
4 P |
|
|
Aufgabe 4b: |
In einem
Viereck ABCD sind die Seiten
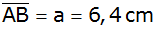 und
und
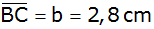 sowie die Winkel
sowie die Winkel
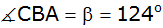 und
und
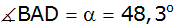 bekannt. Der Flächeninhalt des Teildreiecks ACD
beträgt
bekannt. Der Flächeninhalt des Teildreiecks ACD
beträgt
 . . |
Berechnen Sie
die Diagonale
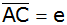 und die Seite
und die Seite
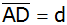 . . |
|
|
4 P |
|
|
Aufgabe 4c: |
Durch die Seiten
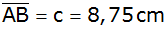 und und
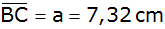 sowie
dem Winkel sowie
dem Winkel
 sind
zwei nichtkongruente Dreiecke gegeben. sind
zwei nichtkongruente Dreiecke gegeben. |
| Wieviel Prozent der Fläche des
größeren Dreiecks nimmt die Fläche des kleineren Dreiecks
ein? |
|
3 P |
|
|
Aufgabe 5a: |
| 1. |
Bestimmen Sie die Definitionsmenge
und die Lösungsmenge der Gleichung |
| |
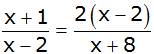 . . |
| 2. |
Die Gleichung
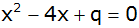 hat die
Lösungen hat die
Lösungen  und
und  mit mit
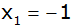 . . |
| |
Wie groß sind
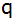 und
und  ? ? |
|
|
4 P |
|
|
Aufgabe 5b: |
| 1. |
Für welche Werte von k hat die
Gleichung |
| |
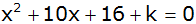 |
| |
zwei, eine bzw. keine reellen Lösungen? |
| 2. |
Für welche Werte von k hat die
Gleichung |
|
 |
| |
nur eine (zusammenfallende) reelle
Lösung? |
| |
Geben Sie die entsprechenden
Gleichungen an. |
|
|
4 P |
|
|
Aufgabe 5c: |
Die Seite
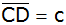 eines Trapezes ABCD ist 7 cm lang. Die parallele
Seite
eines Trapezes ABCD ist 7 cm lang. Die parallele
Seite
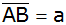 ist um x cm länger und die
ist um x cm länger und die
Höhe h des Trapezes um
x cm kürzer als die Seite c. Der Flächeninhalt des
Trapezes beträgt
 . . |
| Berechnen Sie
die Maßzahlen der Seite a und der Höhe h dieses
Trapezes. |
|
|
3 P |
|
|
Aufgabe 6a: |
| Frau Mayer hat 45.800 DM auf einem
Sparkonto. Sie bekommt dafür jährlich 8,5% Zinsen. Von
diesen Zinsen sind 600 DM steuerfrei, vom Rest muß sie 22%
Steuern bezahlen. |
| Auf welchen Betrag hat sich das
Guthaben von Frau Mayer nach Abzug der Steuern erhöht? |
| Um wieviel Prozent erhöhte sich das
Guthaben von Frau Mayer tatsächlich? |
|
|
4 P |
|
|
Aufgabe 6b: |
| Nachdem ein Fußballverein die
Meisterschaft errungen hatte, verlor er in den
darauffolgenden Jahren jeweils 17% der Zuschauerzahl des
Vorjahres. Als die Zuschauerzahl gegenüber dem
Meisterschaftsjahr auf weniger als die Hälfte zurückgegangen
war, ergriff der Verein Maßnahmen, durch die es gelang, die
Zuschauerzahl wieder jährlich um 12% gegenüber der
jeweiligen Vorjahresanzahl zu erhöhen. |
| Berechnen Sie tabellarisch, nach wie
vielen Jahren die Zuschauerzahl erstmals weniger als die
Hälfte betrug. |
| Wie viele Jahre mußte die
Zuschauerzahl dann zunehmen, bis der ursprüngliche
Spitzenwert erstmals übertroffen wurde? |
| Im 3. Jahre der Zunahme kamen 303272
Zuschauer. |
| Berechnen Sie die kleinste
Zuschaueranzahl dieses Vereins während eines Jahres. |
|
|
4 P |
|
|
Aufgabe 6c: |
| 1. |
Ein Taschenbuch hat 180 Seiten und
durchschnittlich auf jeder Seite 36 Zeilen. Eine zweite
Auflage wird gedruckt, 5 Zeilen der ersten Auflage ergeben
jetzt 8 Zeilen. Auf jeder Seite befinden sich nun durch-
schnittlich 24 Zeilen. |
| |
Wie viele Seiten hat ein Buch der zweiten Auflage? |
| |
Um wieviel Prozent erhöhte sich die Seitenanzahl? |
| 2. |
Das Buch wird in der dritten Auflage
mit einer kleineren Seitenanzahl gedruckt. Dazu werden
jeweils zwei
Seiten der zweiten Auflage so verkleinert,
daß sie zusammen nur noch ein Viertel einer neuen Seite aus-
machen. |
|
Wie viele Seiten hat das Buch jetzt? |
|
|
3 P |
|