|
Aufgabe 1a: |
Eine
quadratische Pyramide ist durch ihr Volumen
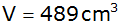 und ihre Höhe
und ihre Höhe
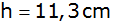 gegeben.
gegeben. |
Skizzieren Sie
ein Schrägbild und kennzeichnen Sie darin die
Grundkante a, die Pyramidenhöhe h, die
Seitenflächenhöhe
 und die Seitenkante s.
und die Seitenkante s. |
Berechnen Sie
a,
 und O dieser Pyramide.
und O dieser Pyramide. |
|
|
4 P |
|
|
Aufgabe 1b: |
Ein
quadratischer Pyramidenstumpf ist durch sein Volumen
 ,
seine Höhe ,
seine Höhe
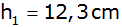 und seine Grundkante
und seine Grundkante
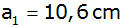 gegeben.
gegeben. |
Berechnen Sie
die Deckkante
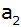 des Pyramidenstumpfes und die Höhe
des Pyramidenstumpfes und die Höhe
 der Ergänzungspyramide.
der Ergänzungspyramide. |
|
|
4 P |
|
|
Aufgabe 1c: |
Ein
quadratischer Pyramidenstumpf ist durch seine
Grundkante
 ,
die Deckkante ,
die Deckkante
 und die Höhe
und die Höhe
 mit
mit
 gegeben.
gegeben. |
| Berechnen Sie
die Oberfläche O dieses Pyramidenstumpfes in
Abhängigkeit von e. |
Für welchen
Wert von e ist
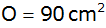 ? ? |
|
|
3 P |
|
|
Aufgabe 2a: |
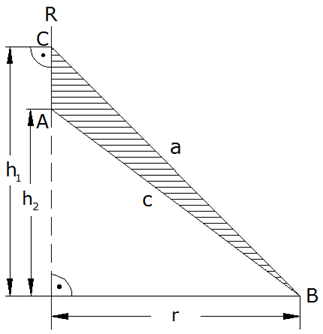
| Das Dreieck ABC
rotiert um die Achse R (siehe nebenstehende
Abbildung). |
Gegeben sind
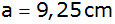 , ,
 und
und
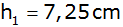 . . |
Berechnen Sie
den Radius r, die Höhe
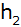 und das Volumen V des Rotationskörpers.
und das Volumen V des Rotationskörpers. |
|
|
 |
4 P |
|
|
Aufgabe 2b: |
In einem
rechtwinkligen Koordinatensystem (Längeneinheit 1
cm) ist das Dreieck ABC durch
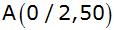 , ,
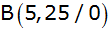 und
und
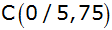 gegeben.
gegeben. |
Berechnen Sie
die Seiten
 und
und
 . . |
| Wie groß ist
die Oberfläche O des Rotationskörpers, der bei
Drehung des Dreiecks um die x-Achse entsteht? |
|
|
4 P |
|
|
Aufgabe 2c: |
In einem
rechtwinkligen Koordinatensystem (Längeneinheit 1
cm) ist das Dreieck ABC durch
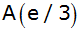 , ,
 und
und
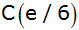 mit
mit
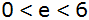 gegeben.
gegeben. |
Weisen Sie
nach, daß für das Volumen V des Rotationskörpers,
der bei Drehung des Dreiecks ABC um die y-Achse
entsteht, die Formel
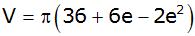 gilt.
gilt. |
Für welchen
Wert von e ist
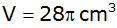 ? ? |
|
|
3 P |
|
|
Aufgabe 3a: |
Das Viereck
ABCD wird durch die Diagonale
 in ein rechtwinkliges und ein gleichschenkliges
Dreieck zerlegt (siehe nebenstehende Abbildung).
in ein rechtwinkliges und ein gleichschenkliges
Dreieck zerlegt (siehe nebenstehende Abbildung). |
Der Umfang des
Vierecks ABCD beträgt 23,5 cm;
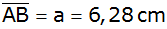 , ,
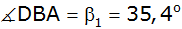 . . |
Berechnen Sie
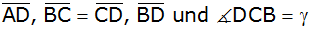 . . |
|
|
 |
4 P |
|
|
Aufgabe 3b: |
Ein Viereck
ABCD ist durch
 , ,
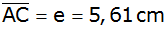 , ,
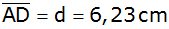 , ,
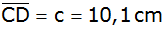 und
und
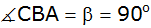 gegeben.
gegeben. |
Zeichnen Sie
diese Figur maßstabgerecht und bestimmen Sie die
Winkel
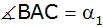 und
und
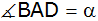 . . |
|
|
4 P |
|
|
Aufgabe 3c: |
Von einem
Viereck ABCD sind gegeben:
 , ,
 , ,
 , ,
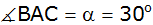 . . |
Weisen Sie
nach, daß sich der Umfang u und der Flächeninhalt A
des Vierecks nach den Formeln
 , ,
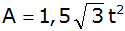 berechnen
lassen. berechnen
lassen. |
Welchen Wert
nimmt t an, wenn der Flächeninhalt des Vierecks  beträgt?
beträgt? |
|
|
3 P |
|
|
Aufgabe 4a: |
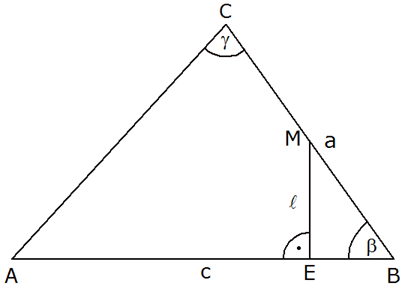
Gegeben ist das
Dreieck ABC mit den Winkeln
 und
und
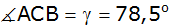 .
Das Lot vom Mittelpunkt M der Seite .
Das Lot vom Mittelpunkt M der Seite
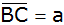 auf die Seite
auf die Seite
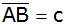 schneidet diese in E (siehe nebenstehende
Abbildung), seine Länge
schneidet diese in E (siehe nebenstehende
Abbildung), seine Länge
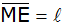 beträgt 3,45 cm.
beträgt 3,45 cm. |
Zeichnen Sie
dieses Dreieck maßgerecht und berechnen Sie die
Längen der Seiten
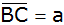 und
und
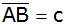 sowie den Flächeninhalt A des Dreiecks.
sowie den Flächeninhalt A des Dreiecks. |
|
|
 |
4 P |
|
|
Aufgabe 4b: |
In einem Dreieck ABC läßt sich der Umkreisradius r
mit der Formel
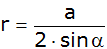 berechnen.
berechnen. |
Tabellieren Sie für das Dreieck ABC im Intervall
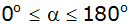 die Abhängigkeit der Seitenlänge
die Abhängigkeit der Seitenlänge
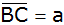
vom Winkel
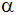 in Schritten von
in Schritten von
 ,
wenn der Umkreisradius ,
wenn der Umkreisradius
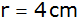 beträgt.
beträgt. |
Stellen Sie diese Abhängigkeit in einem
rechtwinkligen Koordinatensystem graphisch dar
(Abszisse: Winkel
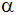 , ,
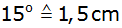 ;
Ordinate: Seitenlänge a, ;
Ordinate: Seitenlänge a,
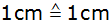 ). ). |
Bestimmen Sie mit Hilfe des Graphen die Winkel
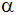 ,
die zur Seitenlänge ,
die zur Seitenlänge
 gehören.
gehören. |
|
|
4 P |
|
|
Aufgabe 4c: |
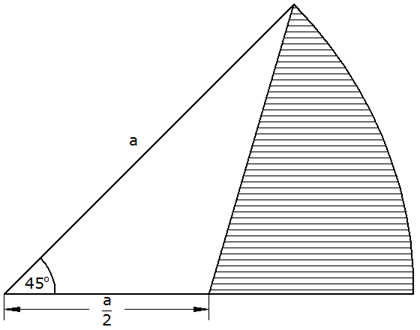
| In
nebenstehender Figur soll der Inhalt der
schraffierten Fläche in Abhängigkeit von a berechnet
werden. |
Zeigen Sie, daß
für ihn
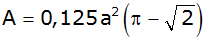 gilt.
gilt. |
Wie groß wird
a, wenn der Flächeninhalt des schraffierten
Figurenteiles
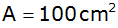 beträgt?
beträgt? |
|
|
 |
3 P |
|
|
Aufgabe
5a: |
| 1. |
Bestimmen Sie die
Definitionsmenge und die Lösungsmenge der Gleichung
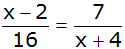 . . |
| 2. |
Die Gleichung
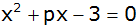 hat die Lösung
hat die Lösung
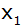 und
und
 mit
mit
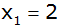 . . |
| |
Bestimmen Sie
 und
und
 . . |
|
|
|
4 P |
|
|
Aufgabe
5b: |
| 1. |
Für welche Werte von k hat
die Gleichung
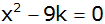 keine reellen Lösungen?
keine reellen Lösungen? |
|
2. |
Für welchen Wert von k hat
die Gleichung
 zwei (gleiche) reelle Lösungen?
zwei (gleiche) reelle Lösungen? |
| |
Geben Sie die zugehörige
Gleichung an. |
|
|
|
4 P |
|
|
Aufgabe
5c: |
| Für vier
aufeinanderfolgende gerade (natürliche) Zahlen gilt: |
| Dividiert man
das Produkt der beiden letzten Zahlen durch das Produkt der
beiden ersten Zahlen, so beträgt der Quotient 2,5. |
| Berechnen Sie
diese vier Zahlen. |
|
|
3 P |
|
|
Aufgabe 6a: |
| Ein
Einfamilienhaus hatte im Jahre 1975 einen Schätzwert von
240.000 DM. |
| Stellen Sie die
Entwicklung des Hauswertes in vollen Beträgen tabellarisch
bis 1978 dar, wenn eine durchschnittliche Wertsteigerung von
jährlich 5% angenommen wird. |
| Handelt es sich
dabei um ein lineares oder ein exponentielles Wachstum
(Begründung)? |
| Um wieviel
Prozent stieg der Wert des Hauses in dem angegebenen
Zeitraum? |
|
|
4 P |
|
|
Aufgabe 6b: |
| In einem
Betrieb werden von einer Maschine A täglich 28000 Teile
angefertigt, von denen durchschnittlich 5,5% fehlerhaft
sind. Von einer zweiten Maschine B, deren Fehlerquote
durchschnittlich 6,5% beträgt, werden täglich 18000 Teile
derselben Art angefertigt. |
| Wie hoch ist
die Anzahl der fehlerhaften Teile, die täglich anfallen? |
| Bestimmen Sie
den prozentualen Anteil der fehlerhaften Stücke beider
Maschinen. |
| Welche
durchschnittliche Fehlerquote dürfte Maschine B höchstens
haben, wenn beide Maschinen zusammen höchstens 5% Ausschuß
produzieren sollen? |
|
|
4 P |
|
|
Aufgabe 6c: |
| Die DIN-A
Papierformate entstehen durch jeweiliges Halbieren der
Blätter, wobei jeweils die vorherige Breite die nachfolgende
Länge ist. Sie beginnen mit DIN-A-0, es folgen DIN-A-1,
DIN-A-2 usw. |
| 1. |
Um wieviel Prozent ist der Flächeninhalt beim
Format DIN-A-4 kleiner als beim Format DIN-A-0? |
| 2. |
Beim Format DIN-A-5 sind die Maße 148 mm und 210
mm. Geben Sie die Maße vom Format DIN-A-1 an. |
|
|
|
3 P |
|