|
Aufgabe 1a: |
| Das
nebenstehende Parallelogramm ABCD rotiert um die
Achse R. |
Berechnen Sie
das Volumen
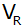 des Rotationskörpers als Vielfaches von
des Rotationskörpers als Vielfaches von
 . . |
| Maße: |
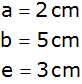 |
|
|
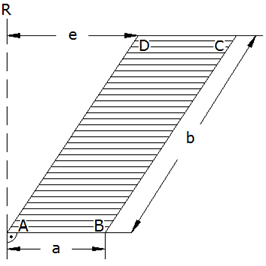 |
4 P |
|
|
Aufgabe 1b: |
In einem
rechtwinkligen Koordinatensystem (Längeneinheit 1
cm) ist ein Parallelogramm A'B'C'D' durch die
Koordinaten seiner Eckpunkte
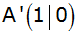 , ,
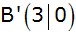 , ,
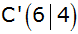 und und
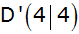 gegeben. Dieses
Parallelogramm gegeben. Dieses
Parallelogramm
rotiert um die y-Achse. |
Berechnen Sie
die Oberfläche des Rotationskörpers als Vielfaches
von
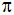 . . |
|
|
4 P |
|
|
Aufgabe 1c: |
In einem
rechtwinkligen Koordinatensystem (Längeneinheit 1
cm) ist ein Parallelogramm A''B''C''D'' durch die
Koordinaten seiner Eckpunkte
 , ,
 , ,
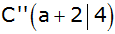 und und
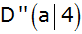 mit
mit
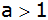 gegeben. Dieses
Parallelogramm rotiert um die y-Achse. gegeben. Dieses
Parallelogramm rotiert um die y-Achse. |
Berechnen Sie
das Volumen
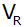 des Rotationskörpers
in Abhängigkeit von a als Vielfaches
von des Rotationskörpers
in Abhängigkeit von a als Vielfaches
von
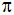 . . |
Wie groß ist a
für
 ? ? |
|
|
3 P |
|
|
Aufgabe 2a: |
| Eine
quadratische Pyramide wird senkrecht zur Grundfläche
so geschnitten, dass die Schnittebene von zwei
gegenüberliegenden Grundkanten gleichen Abstand hat.
Der entstehende Achsenschnitt stellt ein
rechtwinklig-gleichschenkliges Dreieck mit der
Hypotenuse a = 6 cm dar. |
Berechnen Sie die Seitenflächenhöhe
 ,
die Körperhöhe h, das Volumen V und die Mantelfläche
M dieser Pyramide. ,
die Körperhöhe h, das Volumen V und die Mantelfläche
M dieser Pyramide. |
|
|
4 P |
|
|
Aufgabe 2b: |
Ein Kegelstumpf
mit dem Grundkreisradius
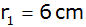 und der Höhe
und der Höhe
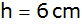 hat ein Volumen
hat ein Volumen
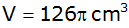 . . |
Wie groß sind der Deckkreisradius
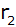 und die Oberfläche O dieses Kegelstumpfes?
und die Oberfläche O dieses Kegelstumpfes? |
|
|
4 P |
|
|
Aufgabe 2c: |
Nebenstehende Abbildung stellt
einen Diagonalschnitt durch eine quadratische
Pyramide, der eine Halbkugel umbeschrieben ist, dar.
Das Volumen dieser Halbkugel beträgt
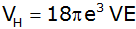 . . |
|
Berechnen Sie den Radius r der Halbkugel und die
Grundkante a der Pyramide in Abhängigkeit von e. |
Für welchen Wert von e hat die Pyramide ein Volumen
von
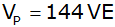 ? ? |
|
|
 |
3 P |
|
|
Aufgabe 3a: |
Die Grundfläche
eines
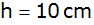 hohen senkrechten Prismas ist ein Dreieck ABC mit
der Seite
hohen senkrechten Prismas ist ein Dreieck ABC mit
der Seite
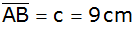
und den Winkeln
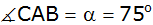 sowie
sowie
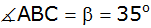 . . |
|
Berechnen Sie die beiden anderen Seiten des Dreiecks
und die Mantelfläche des Körpers. |
|
|
4 P |
|
|
Aufgabe 3b: |
Die Grundfläche
eines Prismas ist ein Dreieck ABC mit den Seiten
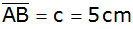 und
und
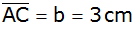
sowie dem Winkel
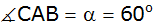 .
Diesem Prisma ist ein Zylinder mit dem Volumen .
Diesem Prisma ist ein Zylinder mit dem Volumen
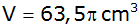 umbeschrieben.
umbeschrieben. |
Berechnen Sie die Seite
 des Dreiecks sowie den Radius r und die Höhe h des
Zylinders.
des Dreiecks sowie den Radius r und die Höhe h des
Zylinders. |
|
|
4 P |
|
|
Aufgabe 3c: |
Gegeben ist die
Funktion
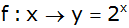 . . |
| 1) |
Ergänzen Sie die Wertetabelle: |
| |
|
| 2) |
Zeichnen Sie den Graphen dieser Funktion
im Intervall in ein Koordinatensystem
ein (Längeneinheit 1 cm)
und entnehmen
Sie der Zeichnung die Funktionswerte für
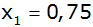 und
und
 . . |
| 3) |
Geben Sie die Funktionsgleichung der
Umkehrfunktion an. |
|
|
|
3 P |
|
|
Aufgabe 3d: |
Ein Rechteck
ABCD ist festgelegt durch
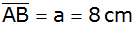 und
und
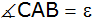 .
Das Rechteck rotiert um die zu .
Das Rechteck rotiert um die zu
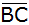 parallele Symmetrieachse.
parallele Symmetrieachse. |
Berechnen Sie das Volumen des entstehenden
Rotationskörpers als Vielfaches von
 in Abhängigkeit von
in Abhängigkeit von
 . . |
Für welchen Wert von
 beträgt das Rotationskörpervolumen
beträgt das Rotationskörpervolumen
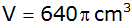 ? ? |
|
|
3 P |
|
|
Aufgabe 4a: |
| Von der
nebenstehender Figur sind gegeben: |
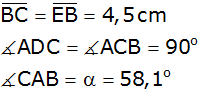 |
| |
Berechnen Sie
 , ,
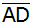 und
und
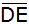 sowie den Abstand des Punktes D von
sowie den Abstand des Punktes D von
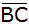 . . |
|
|
 |
4 P |
|
|
Aufgabe 4b: |
Ein Dreieck ABC
ist durch
 , ,
 und
und
 gegeben. Auf
gegeben. Auf
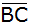 liegt
liegt
Punkt D mit
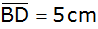 . . |
|
Berechnen Sie den Flächeninhalt des Teildreieckes
ABD. |
|
|
4 P |
|
|
Aufgabe 4c: |
Ein
rechtwinkliges Dreieck ABC mit
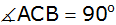 ist durch den Hypotenusenabschnitt
ist durch den Hypotenusenabschnitt
 und den Winkel
und den Winkel
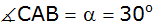 bestimmt.
bestimmt. |
|
Stellen Sie in Abhängigkeit von q eine Formel zur
Berechnung des Flächeninhaltes des Dreieckes auf. |
Welchen Wert nimmt q für
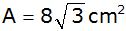 an?
an? |
|
|
3 P |
|
|
Aufgabe 5a: |
| 1) |
Geben Sie alle Lösungen der Aussageform
 im Intervall
im Intervall
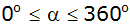 an.
an. |
| 2) |
Stellen Sie
 (deutliche Kennzeichnung!) am Einheitskreis
(1 Längeneinheit = 5 cm) dar
(deutliche Kennzeichnung!) am Einheitskreis
(1 Längeneinheit = 5 cm) dar
und
bestimmen Sie den Wert für x. |
| 3) |
Entscheiden Sie, ob die folgenden
Aussagen wahr (w) oder falsch (f) sind: |
| |
 |
|
|
|
4 P |
|
|
Aufgabe 5b: |
| Von einem
Dreieck ABC sind gegeben: |
 , ,
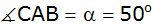 , ,
 . . |
Die Winkelhalbierende
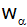 schneidet
schneidet
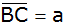 in D. Fällt man von D auf
in D. Fällt man von D auf
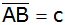 und auf
und auf
 die
die
Lote, so erhält man einen Drachen AEDF. |
|
Fertigen Sie eine maßstabgerechte Zeichnung an. |
Berechnen Sie
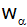 und die Seiten des Drachens.
und die Seiten des Drachens. |
|
|
4 P |
|
|
Aufgabe 5c: |
Gegeben ist
eine Raute ABCD mit dem Umfang
 und dem Winkel
und dem Winkel
 . . |
Zeigen Sie, dass der Flächeninhalt der Raute
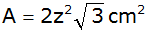 beträgt.
beträgt. |
Für welchen Wert von z beträgt der Flächeninhalt der
Raute
 . . |
|
|
3 P |
|
|
Aufgabe 5d: |
Der
nebenstehende Drachen ABCD ist durch
 , ,
 und
und
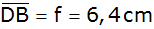 gegeben.
gegeben. |
|
Berechnen Sie die Winkel des Drachens. |
|
|
 |
3 P |
|
|
Aufgabe 6a: |
| Bestimmen Sie
die Lösungsmengen der folgenden Gleichungen: |
| 1. |
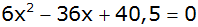 |
| 2. |
 |
|
|
|
4 P |
|
|
Aufgabe 6b: |
| Für welche m
hat die quadratische Gleichung |
|
|
|
genau eine Lösung? |
|
Geben Sie die entstehenden Gleichungen und deren
Lösungen an. |
|
|
4 P |
|
|
Aufgabe 6c: |
| Die Maßzahlen
der Kanten eines Quaders sind drei
aufeinanderfolgende natürliche Zahlen. |
Die Oberfläche dieses Quaders beträgt
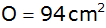 . . |
|
Berechnen Sie die Kanten a, b und c des Quaders. |
|
|
3 P |
|
|
Aufgabe 7a: |
| Subtrahiert man
vom achten Glied einer arithmetischen Reihe das
dritte Glied, so erhält man 20. |
|
Die Summe der ersten zehn Glieder dieser Reihe ist
gleich dem Achtfachen des fünften Gliedes. |
Berechnen Sie d,
 , ,
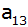 und
und
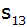 dieser arithmetischen Reihe.
dieser arithmetischen Reihe. |
|
|
4 P |
|
|
Aufgabe 7b: |
Bei einer
anderen arithmetischen Reihe gilt
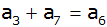 . . |
|
Die Summe der ersten acht Glieder dieser Reihe
beträgt 10. |
Wie groß sind
 und d?
und d? |
Berechnen Sie die Anzahl der Glieder dieser Reihe
für
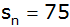 . . |
|
|
4 P |
|
|
Aufgabe 7c: |
In einer
anderen arithmetischen Reihe sind
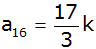 und
und
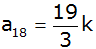 . . |
Wie groß sind
 und d?
und d? |
Zeigen Sie, dass sich in dieser arithmetischen Reihe
für
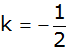 die Summe
die Summe
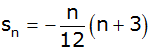 ergibt.
ergibt. |
|
|
3 P |
|