|
Aufgabe 1a: |
|
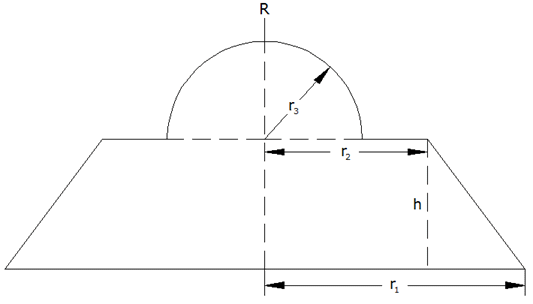
Nebenstehende Figur rotiert um ihre Symmetrieachse. |
Berechnen Sie die Oberfläche des Drehkörpers als
Vielfaches von
 . . |
| Maße: |
 |
|
|
 |
4 P |
|
|
Aufgabe 1b: |
Gegeben
ist das Rechteck ABCD mit den Seiten
 und
und
 . . |
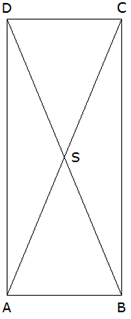
| Die
Diagonalen schneiden sich in S (siehe nebenstehende
Skizze). |
Das
Teildreieck ASD rotiert um die Seite
 . . |
Berechnen Sie das Volumen des Drehkörpers als
Vielfaches von
 . . |
|
|
 |
4 P |
|
|
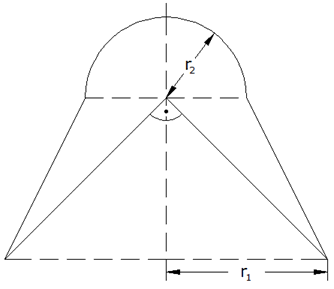
Aufgabe 1c: |
Ein
Werkstück (siehe nebenstehende Figur) hat ein
Volumen von
 . . |
Die
Halbkugel hat den Radius
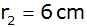 . . |
Berechnen Sie den Radius
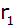 des ausgefrästen Kegels.
des ausgefrästen Kegels. |
|
|
 |
3 P |
|
|
Aufgabe 2a: |
Von einem
gleichschenkligen Trapez ABCD sind die Grundseite
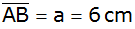 ,
die dazu parallele Seite ,
die dazu parallele Seite
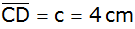 und der Flächeninhalt
und der Flächeninhalt
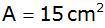 gegeben.
gegeben. |
| Berechnen Sie
die Trapezhöhe h. |
| Das Trapez
rotiert um die Seite a. |
Berechnen Sie
das Volumen des Rotationskörpers als Vielfaches von
 . . |
|
|
4 P |
|
|
Aufgabe 2b: |
Von einem
gleichschenkligen Trapez ABCD sind die Seite
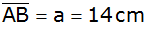 ,
die dazu parallele Seite ,
die dazu parallele Seite
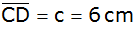 sowie die Höhe
sowie die Höhe
 gegeben.
gegeben. |
| Das Trapez
rotiert erstens um seine Symmetrieachse, zweitens um
die Seite c. |
Berechnen Sie
die Oberflächen beider Rotationskörper als
Vielfaches von
 . . |
|
|
4 P |
|
|
Aufgabe 2c: |
Von einem
gleichschenkligen Trapez ABCD sind die Seite
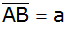 ,
die dazu parallele Seite ,
die dazu parallele Seite
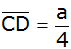 und
und
die Höhe
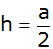 gegeben.
gegeben. |
| Das Trapez
rotiert um die Symmetrieachse. |
Berechnen Sie
das Volumen des Rotationskörpers als Vielfaches von
 . . |
Für welchen
Wert von a ist das Volumen des Rotationskörpers
 Volumenseinheiten groß?
Volumenseinheiten groß? |
|
|
3 P |
|
|
Aufgabe 3a: |
Ein Rechteck
ABCD ist durch die Diagonale
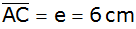 und den Winkel
und den Winkel
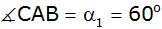 gegeben.
gegeben. |
| Berechnen Sie
die Seiten dieses Rechteckes. |
Das Teildreieck
ACD rotiert um die Rechteckseite
 . . |
Berechnen Sie
das Volumen dieses Rotationskörpers als Vielfaches von
 . . |
|
|
4 P |
|
|
Aufgabe 3b: |
Ein Prisma mit
der quadratischen Grundfläche ABCD ist durch seine
Höhe
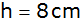 und seine Oberfläche
und seine Oberfläche
 gegeben.
gegeben. |
| Berechnen Sie
die Grundkante a. |
| S sei der
Diagonalschnittpunkt der Deckfläche des Prismas. |
Berechnen Sie
den Winkel
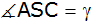 . . |
|
|
4 P |
|
|
Aufgabe 3c: |
| 1) |
Der Graph der Funktion
 mit
mit
 geht durch den Punkt
geht durch den Punkt
 . . |
| 2) |
Wie erhält man ohne Wertetabelle den
Graphen der Umkehrfunktion zur Funktion:
 mit
mit
 ,
wenn der Graph dieser Funktion in einem
rechtwinkligen Koordinatensystem
eingezeichnet ist? ,
wenn der Graph dieser Funktion in einem
rechtwinkligen Koordinatensystem
eingezeichnet ist? |
| 3) |
Wie lautet die Funktionsgleichung der
Umkehrfunktion zur Funktion:
 mit
mit
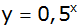 ? ? |
|
|
|
3 P |
|
|
Aufgabe 3d: |
In einem
rechtwinkligen Koordinatensystem (Längeneinheit 1
cm) ist das Dreieck ABC durch die Punkte
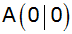 , ,
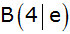 und
und
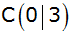 mit
mit
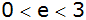 gegeben.
gegeben. |
| Das Dreieck
rotiert erstens um die x-Achse und zweitens um die
y-Achse. |
Berechnen Sie
die Volumen
 und
und
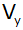 als Vielfaches von als Vielfaches von
 . . |
Für welchen
Wert von e gilt
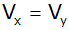 ? ? |
|
|
3 P |
|
|
Aufgabe 4a: |
In einem gleichschenkligen Dreieck ABC mit
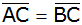 erhält man die Strecke
erhält man die Strecke
 dadurch, dass man den Eckpunkt A mit dem Mittelpunkt
P der Höhe
dadurch, dass man den Eckpunkt A mit dem Mittelpunkt
P der Höhe
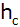 verbindet (siehe nebenstehende Skizze).
verbindet (siehe nebenstehende Skizze). |
Der Winkel
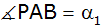 beträgt
beträgt
 . . |
Berechnen Sie die Länge der Höhe
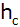 ,
den Flächeninhalt A sowie die Winkel des Dreiecks
ABC. ,
den Flächeninhalt A sowie die Winkel des Dreiecks
ABC. |
|
|
 |
4 P |
|
|
Aufgabe 4b: |
Von einem
gleichschenkligen Dreieck ABC sind die Schenkel
 und der Winkel
und der Winkel
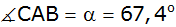 gegeben.
gegeben. |
Berechnen Sie
die Länge der Seite
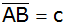 und der Seitenhalbierenden
und der Seitenhalbierenden
 . . |
|
|
4 P |
|
|
Aufgabe 4c: |
Gegeben ist ein
gleichschenkliges Dreieck ABC mit der Basis
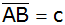 und dem Winkel
und dem Winkel
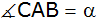 . . |
Zeigen Sie,
dass der Umfang des Dreiecks in Abhängigkeit von
diesen Größen
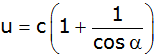 beträgt.
beträgt. |
Für welchen
Wert von
 beträgt der Umfang
beträgt der Umfang
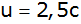 ? ? |
|
|
3 P |
|
|
Aufgabe 5a: |
| 1. |
Beweisen Sie:
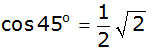 . . |
| 2. |
Der Sinus eines Winkels im Intervall
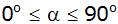 beträgt
beträgt
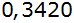 . .
Berechnen Sie den Kosinus dieses Winkels. |
| 3. |
Für welchen Winkel im Intervall
 ist der Term
ist der Term
 nicht definiert?
nicht definiert? |
| 4. |
Übertragen Sie die folgenden Aufgaben
auf Ihr Arbeitsblatt. Fügen Sie eines der
Relations-
zeichen < , = , > so an Stelle
des Fragezeichens ein, dass eine wahre
Aussage entsteht:
 |
|
|
|
4 P |
|
|
Aufgabe 5b: |
Ein Dreieck ABC
ist gegeben durch
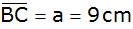 , ,
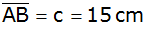 und Winkel
und Winkel
 . . |
Berechnen Sie
die fehlenden Winkel, die Seite
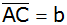 und den Flächeninhalt dieses Dreieckes.
und den Flächeninhalt dieses Dreieckes. |
|
|
4 P |
|
|
Aufgabe 5c: |
In einem
gleichschenkligen Trapez ABCD ist die Grundseite
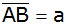 um 6 cm länger als die Seite
um 6 cm länger als die Seite
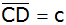 . .
Der Basiswinkel
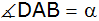 beträgt
beträgt
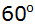 . . |
Zeigen Sie,
dass die Höhe des Trapezes
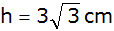 beträgt.
beträgt. |
Für welchen
Wert von a beträgt die Länge der Diagonalen
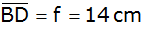 ? ? |
|
|
3 P |
|
|
Aufgabe 5d: |
In dem Trapez
ABCD ist
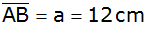 , ,
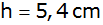 , ,
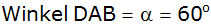 und
und
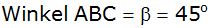 . . |
Berechnen Sie
die Seiten
 und
und
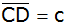 sowie den Flächeninhalt dieses Trapezes.
sowie den Flächeninhalt dieses Trapezes. |
|
|
4 P |
|
|
Aufgabe 6a: |
| 1. |
Lösen Sie die Gleichung
 . . |
| 2. |
Die Gleichung
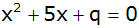 hat zwei ganzzahlige Lösungen. Die erste
Lösung ist
hat zwei ganzzahlige Lösungen. Die erste
Lösung ist
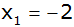 . .
Bestimmen Sie den Wert q und die zweite
Lösung
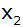 . . |
|
|
|
4 P |
|
|
Aufgabe 6b: |
| 1. |
Bestimmen Sie die Lösungsmenge der
Gleichung
 . . |
| 2. |
Wie heißt die Normalform der
quadratischen Gleichung mit den Lösungen
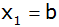 und
und
 ? ? |
|
|
|
4 P |
|
|
Aufgabe 6c: |
Gegeben ist ein Rechteck ABCD mit
 und
und
 . . |
Um welche Strecke x muss man die längere Seite
verkleinern und gleichzeitig die kürzere vergrößern,
damit ein neues Rechteck mit der doppelten Flächen
entsteht? |
|
Geben Sie die Länge und die Breite des neuen
Rechteckes an. |
|
|
3 P |
|
|
Aufgabe 7a: |
| Subtrahiert man
vom siebten Glied einer arithmetischen Reihe das
fünfte Glied, so erhält man 8. |
|
Die Summe aus dem dritten bis fünften Glied ergibt
das siebte Glied. |
|
Die Reihe hat acht Glieder. |
Berechnen Sie d,
 , ,
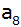 und
und
 . . |
|
|
4 P |
|
|
Aufgabe 7b: |
| Subtrahiert man
in einer anderen aritmetischen Reihe das dritte
Glied vom siebten Glied, so erhält man 10. |
|
Dividiert man die Summe aus dem vierten und sechsten
Glied durch das erste Glied, so ergibt sich 12. |
Berechnen Sie d und
 . . |
|
Die Summe aller Glieder beträgt 108. |
|
Berechnen Sie n. |
|
|
4 P |
|
|
Aufgabe 7c: |
Eine
arithmetische Reihe ist gegeben durch
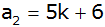 und
und
 . . |
Berechnen Sie d und
 . . |
Für welchen Wert von k gilt
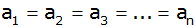 ? ? |
|
|
3 P |
|