|
Aufgabe 1a: |
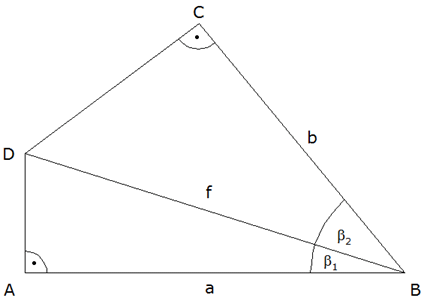
Von einem Viereck ABCD sind die Winkel
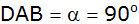 , ,
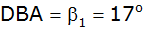 und
und
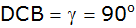 ,
sowie die Seiten ,
sowie die Seiten
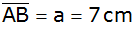 und
und
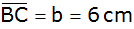 gegeben.
gegeben. |
Berechnen Sie
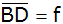 , ,
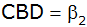 und den Umfang des Vierecks ABCD.
und den Umfang des Vierecks ABCD. |
|
|
 |
4 P |
|
|
Aufgabe 1b: |
|
Ein Trapez ABCD hat folgende Maße: |
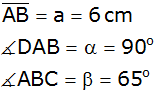 |
Die Winkelhalbierende
 ist gleichzeitig Diagonale
ist gleichzeitig Diagonale
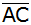 . . |
|
Berechnen Sie den Umfang des Trapezes. |
|
|
 |
4 P |
|
|
Aufgabe 1c: |
Ein
gleichschenkliges Dreieck ABC ist im rechtwinkligen
Koordinatensystem (LE = 1 cm) durch
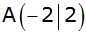 , ,
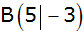 , ,
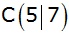 gegeben.
gegeben. |
| Zeichnen Sie
das Dreieck mit seinem Umkreis in das
Koordinatensystem. |
| Berechnen Sie
den Radius r des Umkreises. |
|
|
3 P |
|
|
Aufgabe 2a: |
Von einem
Trapez ABCD sind die Grundseite
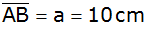 ,
die Seite ,
die Seite
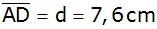 ,
sowie ,
sowie
die Winkel
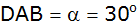 und
und
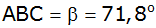 gegeben.
gegeben. |
| Zeichnen Sie
das Trapez maßstabgerecht. |
| Berechnen Sie
seinen Flächeninhalt. |
|
|
4 P |
|
|
Aufgabe 2b: |
Ein Dreieck ist
durch die Seite
 ,
den Winkel ,
den Winkel
 und die Winkel-
und die Winkel-
halbierende
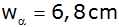 gegeben.
gegeben. |
| Zeichnen Sie
das Dreieck maßstabgerecht. |
Die
Winkelhalbierende
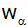 schneidet die Seite
schneidet die Seite
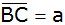 in D.
in D. |
Berechnen Sie
die Länge der Strecke
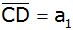 . . |
|
|
4 P |
|
|
Aufgabe 2c: |
|
Gegeben ist ein Quadrat ABCD. |
Berechnen Sie den Inhalt der schraffierten Fläche in
Abhängigkeit von a und
 für
für
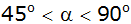 . . |
Für welchen Winkel
 nimmt die schraffierte Fläche zwei Drittel der
Quadratfläche ein?
nimmt die schraffierte Fläche zwei Drittel der
Quadratfläche ein? |
|
|
 |
3 P |
|
|
Aufgabe 3a: |
In zwei
Zylinder mit denselben Maßen (r für den
Grundkreisradius und 2r für die Höhe) sind die
quadratischen Pyramiden
 und
und
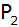 einbeschrieben.
einbeschrieben. |
 |
Berechnen Sie
für
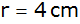 die Rauminhalte beider Pyramiden.
die Rauminhalte beider Pyramiden. |
Wie lang ist
die Seitenkante der Pyramide
 ? ? |
|
|
4 P |
|
|
Aufgabe 3b: |
In zwei
Zylinder mit denselben Maßen (r für den
Grundkreisradius und 2r für die Höhe) sind die
quadratischen Pyramiden
 und
und
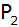 einbeschrieben.
einbeschrieben. |
 |
| Berechnen Sie
die beiden Pyramidenoberflächen in Abhängigkeit von
r. |
|
|
4 P |
|
|
Aufgabe 3c: |
In zwei
Zylinder mit denselben Maßen (r für den
Grundkreisradius und 2r für die Höhe) sind die
quadratischen Pyramiden
 und
und
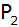 einbeschrieben.
einbeschrieben. |
 |
| Beiden
Pyramiden wird der größtmögliche Kreiskegel
einbeschrieben. |
| Berechnen Sie
das Volumen der einbeschriebenen Kreiskegel in
Abhängigkeit von r. |
|
|
3 P |
|
|
Aufgabe 4a: |
In einem
rechtwinkligen Koordinatensystem (Längeneinheit 1
cm) ist ein Dreieck ABC durch
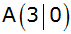 , ,
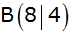 , ,
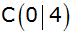 gegeben.
gegeben. |
| Zeichnen Sie
das Dreieck. |
Berechnen Sie
die Länge von
 und
und
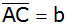 sowie die Winkel des Dreiecks.
sowie die Winkel des Dreiecks. |
|
|
4 P |
|
|
Aufgabe 4b: |
| Die Figur aus
Aufgabe 4a rotiert 1. um die x-Achse und 2. um die
y-Achse. |
Berechnen Sie
die Rauminhalte der beiden Rotationskörper als
Vielfaches von
 . . |
| In welchem
ganzzahligen Verhältnis stehen die Rauminhalte der
beiden Rotationskörper? |
|
|
4 P |
|
|
Aufgabe 4c: |
Ein Dreieck ABC
ist in einem rechtwinkligen Koordinatensystem
(Längeneinheit 1 cm) durch
 , ,
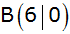 , ,
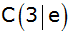 festgelegt, wobei
festgelegt, wobei
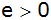 gilt.
gilt. |
| Das Dreieck
rotiert 1. um die x-Achse und 2. um die y-Achse. |
| Welchen
Zahlenwert müsste e annehmen, damit die entstandenen
Rotationskörper denselben Rauminhalt aufweisen? |
|
|
3 P |
|
|
Aufgabe 5a: |
|
1. |
Bestimmen Sie die
Funktionswerte von
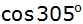 und
und
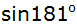 . . |
| 2. |
Bestimmen Sie die
Lösungsmenge der Aussageform
 für
für
 . . |
| 3. |
Beweisen Sie, dass
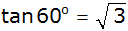 gilt.
gilt. |
|
|
4 P |
|
|
Aufgabe 5b: |
| 1. |
Gegeben ist die Funktion
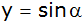 . . |
| |
Tabellieren Sie diese
Funktion mit einer Schrittlänge von
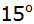 für
für
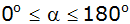 . . |
| 2. |
Zeichnen Sie den Graph
dieser Funktion. |
| |
(Abszisse:
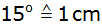 ;
Ordinate: ;
Ordinate:
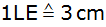 ) ) |
| 3. |
Lesen Sie aus dem Graph ab,
welche Winkel zu dem Funktionswert
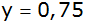 gehören.
gehören. |
|
|
4 P |
|
|
Aufgabe 5c: |
| 1. |
Von einem Dreieck ABC kennt
man die Seiten
 und
und
 sowie den Winkel
sowie den Winkel
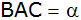 . . |
| |
Leiten Sie in Abhängigkeit
von diesen drei Größen eine Formel zur Berechnung
des Flächeninhaltes
des Dreiecks ABC her. |
| 2. |
Wie lautet die gewonnene
Formel für ein rechtwinkliges Dreieck mit
 ? ? |
|
|
3 P |
|
|
Aufgabe 6a: |
|
1. |
Lösen Sie die quadratische
Gleichung
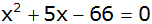 . . |
|
2. |
Eine quadratische Gleichung
hat die beiden Lösungen
 und
und
 . . |
| |
Geben Sie die gesuchte
Gleichung in Normalform an. |
|
|
4 P |
|
|
Aufgabe 6b: |
Die Gleichung
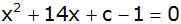 hat
nach Wahl der Variablen c eine verschiedene Anzahl von hat
nach Wahl der Variablen c eine verschiedene Anzahl von
reellen Lösungen. |
|
Für welche Werte von c hat diese Gleichung zwei, eine (zwei
gleiche) oder keine Lösungen? |
|
4 P |
|
|
Aufgabe 6c: |
Die Gleichung
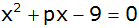 hat die
eine Lösung hat die
eine Lösung
 . . |
Bestimmen Sie die andere Lösung
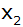 dieser
Gleichung sowie den Wert von p. dieser
Gleichung sowie den Wert von p. |
|
3 P |
|
|
Aufgabe 7a: |
|
Ein Pyramidenstumpf mit quadratischer Grund- und Deckfläche
hat folgende Maße: |
Diagonale der Grundfläche
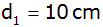 ,
Diagonale der Deckfläche ,
Diagonale der Deckfläche
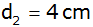 ,
Seitenkante ,
Seitenkante
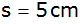 . . |
|
Berechnen Sie die Höhe und das Volumen des
Pyramidenstumpfes. |
|
4 P |
|
|
Aufgabe 7b: |
Eine Seitenfläche eines quadratischen Pyramidenstumpfes ist
ein gleichschenkliges Trapez mit der Höhe
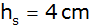 und der
Grundseite und der
Grundseite
 . . |
Welche Länge muss die zu
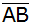 parallele Trapezseite b aufweisen, damit der Pyramidenstumpf
eine Ober-
parallele Trapezseite b aufweisen, damit der Pyramidenstumpf
eine Ober-
fläche von
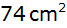 besitzt?
besitzt? |
|
4 P |
|
|
Aufgabe 7c: |
Bei einer Pyramide mit quadratischer Grundfläche ist die
Höhe gleich der Länge der Diagonalen der Grund-
fläche. |
Leiten Sie in Abhängigkeit von der Grundkante a eine Formel
zur Berechnung der Höhe einer Seitenfläche
und der
Oberfläche dieser Pyramide her. |
|
3 P |
|
|
Aufgabe 8a: |
| Subtrahiert man
vom zehnten Glied einer arithmetischen Reihe das
dritte Glied, dann erhält man 14. |
|
Addiert man zum vierten Glied derselben
arithmetischen Reihe das neunte Glied, dann erhält
man sechs. |
|
Diese arithmetische Reihe besitzt 13 Glieder. |
Berechnen Sie die Größen d,
 , ,
 und
und
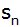 . . |
|
|
4 P |
|
|
Aufgabe 8b: |
| Das siebente
Glied einer anderen arithmetischen Reihe ist halb so
groß wie das zwölfte Glied. |
Berechnen Sie die Größen d und
 ,
wenn ,
wenn
 ist.
ist. |
|
Berechnen Sie weiter n für den Fall, dass die Summe
aller Glieder 360 beträgt. |
|
|
4 P |
|
|
Aufgabe 8c: |
Das erste Glied
einer anderen arithmetrischen Reihe ist
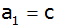 ,
das vierte Glied ist ,
das vierte Glied ist
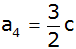 . . |
|
Berechnen Sie d. |
Für welchen Wert von c gilt
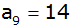 ?
? |
Bestimmen Sie für den so ermittelten Wert von c die
Anzahl aller Glieder dieser Folge, wenn das
vorletzte
Glied
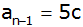 ist.
ist. |
|
|
3 P |
|