|
Aufgabe 1a: |
| Addiert man zum
zweiten Glied einer arithmetischen Reihe das zehnte
Glied, so erhält man 5. |
|
Subtrahiert man vom vierten Glied derselben Reihe
das zehnte Glied, dann erhält man 21. |
|
Die Reihe hat 12 Glieder. |
Berechnen Sie d,
 , ,
 und
und
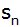 . . |
|
|
4 P |
|
|
Aufgabe 1b: |
| In einer
arithmetischen Reihe ist die Summe aus dem vierten
und sechsten Glied um 1 kleiner als das achte Glied. |
|
Das achte Glied ist das Siebenfache des dritten
Gliedes. |
Ermitteln Sie d und
 . . |
|
Berechnen Sie n für den Fall, dass die Summe aller
Glieder 312 beträgt. |
|
|
4 P |
|
|
Aufgabe 1c: |
Eine arithmetische Reihe mit elf Gliedern besitzt
die Summe
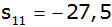 .
Außerdem ist .
Außerdem ist
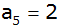 . . |
Streicht man die letzten fünf Glieder dieser Reihe,
so muss zu jedem Glied der verbleinenden Reihe eine
bestimmte Zahl k addiert werden, damit der Wert der
ursprünglichen Summe erhalten bleibt. |
|
Bestimmen Sie die Zahl k. |
|
|
3 P |
|
|
Aufgabe 2a: |
|
Dividiert man das fünfte Glied einer steigenden
geometrischen Reihe durch das zweite Glied, so
erhält man 27. |
|
Die Summe aus dem dritten und vierten Glied beträgt
72. |
Berechnen Sie
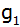 und
und
 dieser Reihe sowie das achte Glied.
dieser Reihe sowie das achte Glied. |
|
Bestimmen Sie die Summe der ersten neun Glieder
dieser Reihe. |
|
|
4 P |
|
|
Aufgabe 2b: |
In einer fallenden geometrischen Reihe ist das
Anfangsglied
 und das fünfte Glied
und das fünfte Glied
 . . |
Berechnen Sie
 . . |
|
Stellen Sie die Reihe bis zum sechsten Glied auf. |
Eine neue geometrische Reihe entsteht dadurch, dass
man bei gleichem Anfangsglied als Quotient den
Kehrwert des oben berechneten
 verwendet.
verwendet. |
|
Wieviele Glieder muss man von dieser Reihe
mindestens addieren, damit ihre Summe größer als
100000 wird? |
|
|
4 P |
|
|
Aufgabe 2c: |
In einer geometrischen Reihe ist der Quotient
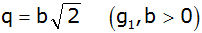 . . |
Das Produkt aus dem zweiten und dritten Glied ist
gleich dem Quotienten
 . . |
Zeigen Sie, dass gilt:
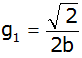 . . |
|
Für welchen Wert von b wird das vierte Glied
der Reihe 50? |
|
|
3 P |
|
|
Aufgabe 3a: |
Von einem
gleichschenkligen Trapez ABCD sind die Grundseite
 ,
die Diagonale ,
die Diagonale
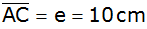 und der Winkel
und der Winkel
 bekannt.
bekannt. |
Berechnen Sie
den Winkel
 ,
die Höhe und die fehlenden Seiten des Trapezes. ,
die Höhe und die fehlenden Seiten des Trapezes. |
|
|
4 P |
|
|
Aufgabe 3b: |
Über der Seite
 eines gleichschenkligen Trapezes ABCD mit
eines gleichschenkligen Trapezes ABCD mit
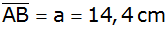 , ,
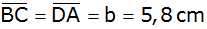 und dem Winkel
und dem Winkel
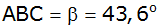 ist ein Kreisbogen gezeichnet mit
ist ein Kreisbogen gezeichnet mit
 als Sehne. Der Mittelpunkt des dazugehörigen Kreises
liegt im Mittelpunkt M der Seite a.
als Sehne. Der Mittelpunkt des dazugehörigen Kreises
liegt im Mittelpunkt M der Seite a. |
| Berechnen Sie
den Radius des Kreisbogens und den Umfang der
Gesamtfigur. |
|
|
4 P |
|
|
Aufgabe 3c: |
Gegeben ist ein
gleichschenkliges Trapez ABCD mit
 , ,
 und dem Winkel
und dem Winkel
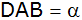 . . |
Leiten Sie
Formeln zur Berechnung von Inhalt und Umfang des
Trapezes in Abhängigkeit von e und
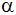 her.
her. |
Welchen Wert
nimmt e an, wenn die Fläche des Trapezes
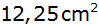 und der Winkel
und der Winkel
 betragen?
betragen? |
|
|
3 P |
|
|
Aufgabe 4a: |
Von einem
Dreieck ABC sind
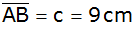 , ,
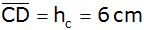 und der Winkel
und der Winkel

gegeben. |
Berechnen Sie
die Strecke
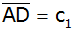 und
und
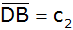 ,
die Seite ,
die Seite
 und den Winkel
und den Winkel
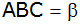 . . |
Auf
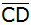 liegt ein Punkt E mit
liegt ein Punkt E mit
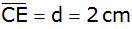 . . |
Welchen Abstand
(kürzeste Entfernung)
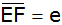 hat dieser Punkt von
hat dieser Punkt von
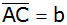 ? ? |
|
|
4 P |
|
|
Aufgabe 4b: |
Berechnen Sie
im Dreieck ABC mit
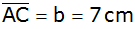 , ,
 und dem Winkel
und dem Winkel
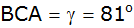
die Länge der Seitenhalbierenden
 und den Winkel
und den Winkel
 . . |
Die
Seitenhalbierende
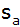 schneidet die Winkelhalbierende des Winkels
schneidet die Winkelhalbierende des Winkels
 in F.
in F. |
Berechnen Sie
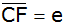 . . |
|
|
4 P |
|
|
Aufgabe 4c: |
In dem Dreieck
ABC mit
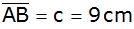 , ,
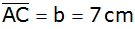 und dem Winkel
und dem Winkel
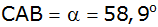 soll auf
soll auf
der Höhe
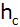 ein Punkt
ein Punkt
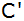 derart bestimmt werden, dass der Winkel
derart bestimmt werden, dass der Winkel
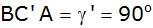 beträgt.
beträgt. |
Zeichnen Sie
das Dreieck ABC maßstabgerecht, konstruieren Sie den
Punkt
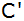 und berechnen Sie den Ab-
und berechnen Sie den Ab-
stand (kürzeste
Entfernung) e des Punktes
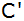 vom Punkt D auf
vom Punkt D auf
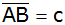 . . |
|
|
3 P |
|
|
Aufgabe 5a: |
In einem
rechtwinkligen Koordinatensystem (Längeneinheit 1
cm) ist ein Viereck ABCD durch
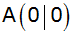 , ,
 , ,
 und
und
 gegeben.
gegeben. |
| Die Figur
rotiert um die x-Achse. |
| Berechnen Sie
die Oberfläche des entstehenden Rotationskörpers. |
|
|
4 P |
|
|
Aufgabe 5b: |
| Die Figur aus
Aufgabe 5a rotiert 1. um die x-Achse und 2. um die
y-Achse. |
| In welchem
Verhältnis stehen die Rauminhalte beider
Rotationskörper? |
(Geben Sie das
Verhältnis in der Form
 an.)
an.) |
|
|
4 P |
|
|
Aufgabe 5c: |
Ein Viereck hat
in einem rechtwinkligen Koordinatensystem
(Längeneinheit 1 cm) die Eckpunkte
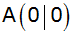 , ,
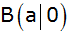 , ,
 und
und
 ; ;
 . . |
| Berechnen Sie
das Volumen des Drehkörpers, den man durch Drehung
der Figur um die y-Achse erhält, in Abhängigkeit von
a. |
| Welche Form hat
dieser Drehkörper, wenn 1.) a zwischen 6 und 10
liegt, 2.) a gleich 6 und 3.) a = 0 ist? |
Welchen Wert
hat a, wenn das Volumen des Drehkörpers
 beträgt?
beträgt? |
|
|
3 P |
|
|
Aufgabe 6a: |
Ein
quadratisches Prisma mit
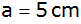 ist
ist
 hoch. Aus diesem Prisma wird eine Pyramide so
herausgearbeitet, dass sich das Volumen des Prismas
um ein Achtel vermindert.
hoch. Aus diesem Prisma wird eine Pyramide so
herausgearbeitet, dass sich das Volumen des Prismas
um ein Achtel vermindert. |
Berechnen Sie
das Volumen
 und die Höhe
und die Höhe
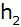 der Pyramide.
der Pyramide. |
| Welche
Oberfläche weist das Prisma nach Herausarbeitung der
Pyramide auf? |
|
|
4 P |
|
|
Aufgabe 6b: |
Einem
quadratischen Prisma mit
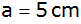 und
und
 wird der größtmögliche Kegel, diesem Kegel
wird der größtmögliche Kegel, diesem Kegel
die
größtmögliche Pyramide mit einem gleichseitigen
Dreieck als Grundfläche einbeschrieben. |
| Berechnen Sie
das Volumen
und die Mantelfläche des Kegels, außerdem das
Volumen der Pyramide. |
|
|
4 P |
|
|
Aufgabe 6c: |
Einem
quadratischen Prisma mit
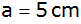 und der Höhe h wird eine Kugel umbeschrieben.
und der Höhe h wird eine Kugel umbeschrieben. |
| Leiten Sie eine
Formel für die Oberfläche dieser Kugel in
Abhängigkeit von h her. |
In welchem
Verhältnis stehen die Oberflächen des Prismas und
der Kugel für
 ? ? |
Geben Sie das
Verhältnis in der Form
 an.
an. |
|
|
3 P |
|
|
Aufgabe 7a: |
|
1. |
Logarithmieren Sie den Term
 und berechnen Sie seinen Wert für a = 100 und b =
25.
und berechnen Sie seinen Wert für a = 100 und b =
25. |
| 2. |
Für welche Basis b gilt
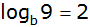 ? ? |
| |
Bestimmen Sie x aus
 . . |
| 3. |
Weisen Sie nach, dass
 gilt.
gilt. |
| 4. |
Drücken Sie durch den
Logarithmus jeweils eines Termes aus: |
| |
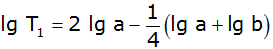 |
| |
und |
| |
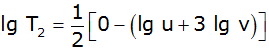 |
|
|
4 P |
|
|
Aufgabe 7b: |
Gegeben ist ein
Graph der Funktion
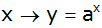 mit
mit
 . . |
 |
|
|
1. |
Entnehmen Sie beliebige
Wertepaare
 und bestimmen Sie damit a.
und bestimmen Sie damit a.
 |
| 2. |
Übertragen Sie obenstehende
Zeichnung und erzeugen Sie punktweise den Graphen
der Umkehrfunktion. |
| |
Geben Sie deren
Funktionsgleichung an. |
| 3. |
Vervollständigen Sie diese
Wertetafel, indem Sie die fehlenden Funktionswerte
dem Graphen der Umkehrfunktion entnehmen. |
| |
| x |
4 |
|
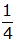 |
 |
|
y |
|
0 |
|
|
|
|
|
4 P |
|
|
Aufgabe 7c: |
|
Ermitteln Sie die Lösungsmengen folgender
Gleichungen: |
|
|
|
|
3 P |
|
|
Aufgabe 8a: |
| 1. |
Bestimmen Sie für
die Winkel
 und
und
 das Bogenmaß.
das Bogenmaß. |
| 2. |
Ermitteln Sie
 und
und
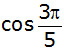 aus der Zahlentafel.
aus der Zahlentafel. |
| 3. |
Berechnen Sie für
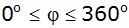 alle Lösungen der Aussageform
alle Lösungen der Aussageform
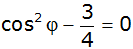 . . |
| 4. |
Beweisen Sie, dass
 gilt.
gilt. |
|
|
|
4 P |
|
|
Aufgabe 8b: |
|
1. |
Drücken Sie die Abhängigkeit der
Standbreite b einer Stehleiter
(siehe nebenstehende Skizze) von der
Länge
 und dem Öffnungswinkel
und dem Öffnungswinkel
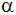 durch eine Formel aus.
durch eine Formel aus. |
 |
|
|
2. |
Tabellieren Sie für
 im Intervall
im Intervall
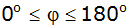 die Abhängigkeit der Standbreite b vom
Winkel
die Abhängigkeit der Standbreite b vom
Winkel
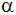 in Schritten von
in Schritten von
 . . |
| |
Stellen Sie diese Abhängigkeit der
Standbreite b von der Winkelgröße
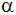 in einem rechtwinkligen Koordinatensystem
graphisch dar (Ordinate:
in einem rechtwinkligen Koordinatensystem
graphisch dar (Ordinate:
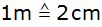 ; Abszisse:
; Abszisse:
 ). ). |
| 3. |
Bestimmen Sie mit Hilfe des Graphen den
Öffnungswinkel
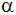 ,
der zur Standbreite ,
der zur Standbreite
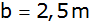 gehört.
gehört. |
|
|
|
4 P |
|
|
Aufgabe 8c: |
Eine Kreissehne
 hat die
Länge 1,7976 LE. Zu ihr gehört ein Mittelpunktswinkel hat die
Länge 1,7976 LE. Zu ihr gehört ein Mittelpunktswinkel
 . . |
|
Bestimmen Sie den Radius r des Kreises. |
|
Der Mittelpunkt dieses Kreises sei M. ABM bildet ein
Dreieck. |
Bestimmen Sie die Dreieckshöhe h auf
 sowie
den Flächeninhalt des Dreiecks. sowie
den Flächeninhalt des Dreiecks. |
Stellen Sie eine Formel für den Flächeninhalt des Dreiecks
ABM im Bereich
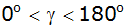 in
Abhängigkeit von in
Abhängigkeit von
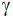 für für
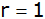 auf. auf. |
|
3 P |
|