|
Aufgabe 1a: |
Für eine
arithmetische Reihe gilt
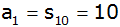 . . |
Berechne die Differenz d und das Glied
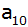 ,
stelle die Reihe auf. ,
stelle die Reihe auf. |
|
|
4 P |
|
|
Aufgabe 1b: |
In einer
arithmetischen Reihe aus sieben Gliedern beträgt die
Summe des vierten und fünften Gliedes 13.
Läßt
man alle Glieder mit geraden Nummern weg, so
besitzen die restlichen Glieder die Summe 32. |
Berechne die Größen d,
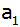 , ,
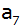 und
und
 dieser Reihe.
dieser Reihe. |
|
|
4 P |
|
|
Aufgabe 1c: |
Die sieben
Glieder einer anderen arithmetischen Reihe haben die
Summe 77, das Produkt des ersten und
siebenten
Gliedes beträgt 40. |
Zeige, dass durch diese Angaben zwei Reihen bestimmt
sind, und gib für beide jeweils die Größen
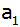 , ,
d und
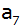 an.
an. |
|
|
3 P |
|
|
Aufgabe 2a: |
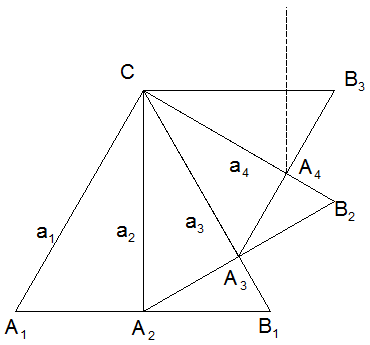
Die Höhe des gleichseitigen Dreiecks
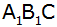 (siehe nebenstehende Skizze) ist Seite eines neuen
gleichseitigen Dreiecks
(siehe nebenstehende Skizze) ist Seite eines neuen
gleichseitigen Dreiecks
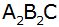 ,
aus dessen Höhe wiederum das gleichseitige Dreieck ,
aus dessen Höhe wiederum das gleichseitige Dreieck
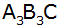 usw. gebildet wird.
usw. gebildet wird. |
Zeichne die ersten fünf Dreiecke dieser Folge mit
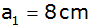 . . |
|
|
 |
3 P |
|
|
Aufgabe 2b: |
Die Höhe des gleichseitigen Dreiecks
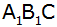 (siehe nebenstehende Skizze) ist Seite eines neuen
gleichseitigen Dreiecks
(siehe nebenstehende Skizze) ist Seite eines neuen
gleichseitigen Dreiecks
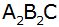 ,
aus dessen Höhe wiederum das gleichseitige Dreieck ,
aus dessen Höhe wiederum das gleichseitige Dreieck
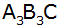 usw. gebildet wird.
usw. gebildet wird. |
Zeige, dass die Dreiecksseiten
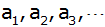 eine geometrische Folge mit
eine geometrische Folge mit
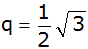 bilden.
bilden. |
|
|
 |
2 P |
|
|
Aufgabe 2c: |
Die Höhe des gleichseitigen Dreiecks
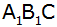 (siehe nebenstehende Skizze) ist Seite eines neuen
gleichseitigen Dreiecks
(siehe nebenstehende Skizze) ist Seite eines neuen
gleichseitigen Dreiecks
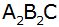 ,
aus dessen Höhe wiederum das gleichseitige Dreieck ,
aus dessen Höhe wiederum das gleichseitige Dreieck
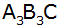 usw. gebildet wird.
usw. gebildet wird. |
Der Punkt
 liegt auf der Strecke
liegt auf der Strecke
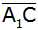 . . |
Berechne für
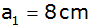 die Länge des Streckenzuges von
die Länge des Streckenzuges von
 bis
bis
 und den Flächeninhalt des Vielecks, das von dem
Streckenzug
und den Flächeninhalt des Vielecks, das von dem
Streckenzug
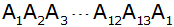 gebildet wird.
gebildet wird. |
|
|
 |
2 P |
|
|
Aufgabe 2d: |
Die Höhe des gleichseitigen Dreiecks
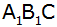 (siehe nebenstehende Skizze) ist Seite eines neuen
gleichseitigen Dreiecks
(siehe nebenstehende Skizze) ist Seite eines neuen
gleichseitigen Dreiecks
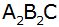 ,
aus dessen Höhe wiederum das gleichseitige Dreieck ,
aus dessen Höhe wiederum das gleichseitige Dreieck
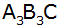 usw. gebildet wird.
usw. gebildet wird. |
Welches Dreieck
 hat für
hat für
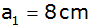 einen Flächeninhalt, der erstmals kleiner als
einen Flächeninhalt, der erstmals kleiner als
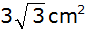 ist?
ist? |
|
|
 |
2 P |
|
|
Aufgabe 3a: |
Von einem Dreieck ABC sind
 , ,
 und
und
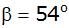 gegeben.
gegeben. |
Konstruiere dieses Dreieck und berechne seine Winkel
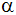 und
und
 sowie seine Seite c.
sowie seine Seite c. |
|
|
4 P |
|
|
Aufgabe 3b: |
Von einem Dreieck ABC sind
 , ,
 und
und
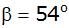 gegeben.
gegeben. |
|
Die Mittelsenkrechte der Seite a schneidet die
benachbarte Seite c im Punkt D. |
|
Berechne den Umfang des Dreiecks BCD. |
|
|
4 P |
|
|
Aufgabe 3c: |
Von einem Dreieck ABC sind
 , ,
 und
und
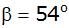 gegeben.
gegeben. |
Konstruiere im Dreieck ABC den Inkreisradius
 und berechne seine Länge.
und berechne seine Länge. |
|
|
3 P |
|
|
Aufgabe 4a: |
In einem rechtwinkligen Koordinatensystem
sind
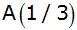 , ,
 und
und
 die Eckpunkte eines Dreiecks.
die Eckpunkte eines Dreiecks. |
|
Zeichne das Dreieck (Längeneinheit 0,5 cm) und weise
rechnerisch nach, dass der Winkel ACB ein rechter
ist. |
|
|
4 P |
|
|
Aufgabe 4b: |
In einem rechtwinkligen Koordinatensystem
sind
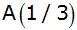 , ,
 und
und
 die Eckpunkte eines Dreiecks.
die Eckpunkte eines Dreiecks. |
Zeige durch Rechnung, dass der Umkreismittelpunkt M
des Dreiecks ABC die Seite
 halbiert, bestimme darüber hinaus die Winkel
halbiert, bestimme darüber hinaus die Winkel
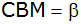 und
und
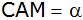 . . |
|
|
4 P |
|
|
Aufgabe 4c: |
In einem rechtwinkligen Koordinatensystem
sind
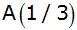 , ,
 und
und
 die Eckpunkte eines Dreiecks.
die Eckpunkte eines Dreiecks. |
Die Winkelhalbierende
 schneidet die Seite
schneidet die Seite
 im Punkt D.
im Punkt D. |
Fälle von den Punkten A und B die Lote auf die
Gerade CD und zeige mithilfe ähnlicher Dreiecke die
Richtigkeit des Streckenverhältnisses
 . . |
|
|
3 P |
|
|
Aufgabe 5a: |
|
In einem rechtwinkligen Koordinatensystem sind vier
Geraden durch die Gleichungen |
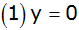 ; ;
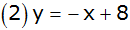 ; ;
 ; ;
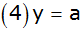 |
|
gegeben. |
Zeige durch Zeichnung (Längeneinheit 1 cm) und
Rechnung, dass die Geraden für
 ein Trapez mit den Eckpunkten
ein Trapez mit den Eckpunkten
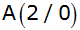 , ,
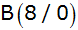 , ,
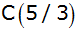 und
und
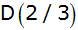 einschließen.
einschließen. |
|
|
4 P |
|
|
Aufgabe 5b: |
|
In einem rechtwinkligen Koordinatensystem sind vier
Geraden durch die Gleichungen |
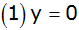 ; ;
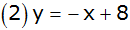 ; ;
 ; ;
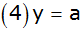 |
|
gegeben. |
Drehe das Trapez ABCD um die x-Achse und bestimme
das Volumen des entstehenden Körpers
als
Vielfaches von
 . . |
|
|
4 P |
|
|
Aufgabe 5c: |
|
In einem rechtwinkligen Koordinatensystem sind vier
Geraden durch die Gleichungen |
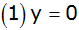 ; ;
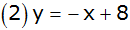 ; ;
 ; ;
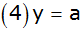 |
|
gegeben. |
Durch die Gerade
 entsteht zusammen mit den anderen Geraden ein
veränderliches
entsteht zusammen mit den anderen Geraden ein
veränderliches
Trapez ABC'D'. |
|
Innerhalb welcher Grenzen kann sich a bewegen? |
|
Welche Koordinaten haben die Punkte C' und D' in
Abhängigkeit von a? |
Welches Volumen hat der durch Drehung des Trapezes
um die x-Achse entstehende Drehkörper
in
Abhängigkeit von a? |
|
|
3P |
|
|
Aufgabe 6a: |
|
Durch die beiden Geraden |
 und
und
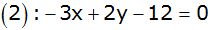 |
|
und die x-Achse ist ein gleichschenkliges Dreieck
bestimmt. |
Zeichne die Geraden in ein rechtwinkliges
Koordinatensystem (Längeneinheit 1 cm) und bestätige
durch
Rechnung die Koordinaten
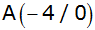 , ,
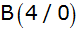 und
und
 der Eckpunkte des Dreiecks.
der Eckpunkte des Dreiecks. |
|
|
4P |
|
|
Aufgabe 6b: |
|
Durch die beiden Geraden |
 und
und
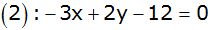 |
|
und die x-Achse ist ein gleichschenkliges Dreieck
bestimmt. |
Berechne vom Dreieck ABC die Winkel
 und
und
 ,
die Seite a und die Seitenhalbierende ,
die Seite a und die Seitenhalbierende
 ; ;
zeige darüber hinaus, dass der Schnittpunkt S
der Seitenhalbierenden diese im Verhältnis 2 : 1
teilt. |
|
|
4P |
|
|
Aufgabe 6c: |
|
Durch die beiden Geraden |
 und
und
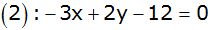 |
|
und die x-Achse ist ein gleichschenkliges Dreieck
bestimmt. |
Schlage um
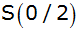 den Kreisbogen zwischen A und B. Er schließt
zusammen mit den Geraden (1)
den Kreisbogen zwischen A und B. Er schließt
zusammen mit den Geraden (1)
und (2) eine Fläche
ein. |
|
Berechne das Volumen des durch Drehung dieser Fläche
um die y-Achse entstehenden Rotationskörpers. |
|
|
3P |
|
|
Aufgabe 7a: |
In einen Würfel mit der Kantenlänge a = 6 cm wird
eine Pyramide eingesetzt. Die Grundfläche dieser
Pyramide entsteht durch Verbindung der Mittelpunkte
der vier unteren Würfelkanten, die Spitze liegt
im Mittelpunkt der oberen Würfelfläche. |
|
Fertige eine Zeichnung an. |
|
Berechne das Volumen der Pyramide und bestimme
dessen prozentualen Anteil am Würfelvolumen. |
|
Aufgabe 7b: |
In einen Würfel mit der Kantenlänge a = 6 cm wird
eine Pyramide eingesetzt. Die Grundfläche dieser
Pyramide entsteht durch Verbindung der Mittelpunkte
der vier unteren Würfelkanten, die Spitze liegt
im Mittelpunkt der oberen Würfelfläche. |
Berechne die Summe aller Kanten der Pyramide und den
Winkel, den jede Seitenfläche mit der Grundfläche
bildet. |
|
|
4P |
|
|
Aufgabe 7c: |
In einen Würfel mit der Kantenlänge a = 6 cm wird
eine Pyramide eingesetzt. Die Grundfläche dieser
Pyramide entsteht durch Verbindung der Mittelpunkte
der vier unteren Würfelkanten, die Spitze liegt
im Mittelpunkt der oberen Würfelfläche. |
Zeige, dass sich für die Oberfläche der Pyramide in
Abhängigkeit von a der Term
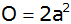 ergibt.
ergibt. |
|
|
3P |
|
|
|
4P |
|
|
Aufgabe 8a: |
Durch Drehung der (nebenstehenden)
schraffierten Fläche um die x-Achse bzw. um
die y-Achse entstehen Drehkörper mit den
Rauminhalten
 bzw.
bzw.
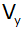 . . |
| |
Zeichne einen Achsenschnitt durch beide
Drehkörper für
a = b = 6 cm und berechne
für diese Werte
 und
und
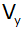
als Vielfaches von
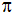 . . |
|
 |
|
|
4P |
|
|
Aufgabe 8b: |
Durch Drehung der (nebenstehenden)
schraffierten Fläche um die x-Achse bzw. um
die y-Achse entstehen Drehkörper mit den
Rauminhalten
 bzw.
bzw.
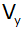 . . |
| |
Stelle für a = 6 cm die
Funktionsgleichungen für
 und
und
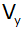 mit der Variablen b auf und ermittle, für
welchen Wert von b die Gleichung
mit der Variablen b auf und ermittle, für
welchen Wert von b die Gleichung
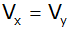 gilt.
gilt. |
|
 |
|
|
|
|
4P |
|
|
Aufgabe 8c: |
Durch Drehung der (nebenstehenden)
schraffierten Fläche um die x-Achse bzw. um
die y-Achse entstehen Drehkörper mit den
Rauminhalten
 bzw.
bzw.
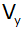 . . |
| |
Leite für b = 2a Formeln für
 und
und
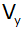 in Abhängigkeit von a her und bestimme das
Zahlenverhältnis beider Rauminhalte.
in Abhängigkeit von a her und bestimme das
Zahlenverhältnis beider Rauminhalte. |
|
 |
|
|
|
|
3P |
|