|
Aufgabe 1a: |
| In einer
arithmetischen Reihe beträgt die Summe der beiden
ersten Glieder 8 und die Summe der beiden letzten
Glieder 32. Das Anfangsglied ist um 14 kleiner als
das Endglied. |
|
Wie heißt die Reihe? |
|
|
4 P |
|
|
Aufgabe 1b: |
| Die Reihe wird
nach links fallend soweit fortgesetzt, bis als neue
Summe 72 entsteht. |
| Wie heißt diese
Reihe? |
|
|
4 P |
|
|
Aufgabe 2a: |
Eine Spirale
entsteht, indem man Halbkreise gleichsinnig drehend
so aneinander setzt, daß der Endpunkt eines
Halbkreises zugleich der Anfangspunkt des nächsten
ist und alle Kreismittelpunkte auf einer Geraden
liegen. Jeder Radius des nachfolgenden Halbkreises
ist um
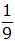 kleiner als der Radius des vorhergehenden
Halbkreises.
kleiner als der Radius des vorhergehenden
Halbkreises. |
Zeichne die
ersten 6 Halbkreise der Spirale, die mit
 beginnt!
beginnt! |
|
|
4 P |
|
|
Aufgabe 2b: |
Eine Spirale
entsteht, indem man Halbkreise gleichsinnig drehend
so aneinander setzt, daß der Endpunkt eines
Halbkreises zugleich der Anfangspunkt des nächsten
ist und alle Kreismittelpunkte auf einer Geraden
liegen. Jeder Radius des nachfolgenden Halbkreises
ist um
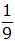 kleiner als der Radius des vorhergehenden
Halbkreises.
kleiner als der Radius des vorhergehenden
Halbkreises. |
| Berechne die
Länge dieser Spirale, wenn sie auf insgesamt 12
Halbkreise nach innen fortgesetzt wird! |
|
|
4 P |
|
|
Aufgabe 2c: |
Eine Spirale
entsteht, indem man Halbkreise gleichsinnig drehend
so aneinander setzt, daß der Endpunkt eines
Halbkreises zugleich der Anfangspunkt des nächsten
ist und alle Kreismittelpunkte auf einer Geraden
liegen. Jeder Radius des nachfolgenden Halbkreises
ist um
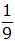 kleiner als der Radius des vorhergehenden
Halbkreises.
kleiner als der Radius des vorhergehenden
Halbkreises. |
| Wie lang wäre
die Spirale, die aus unendlich vielen Halbkreisen
bestehen würde? |
|
|
3 P |
|
|
Aufgabe 3a: |
| Eine
arithmetische und eine geometrische Zahlenfolge
haben dasselbe Anfangsglied 8 und stimmen auch im
zweiten Glied überein. Das dritte Glied der
arithmetischen Zahlenfolge verhält sich zum dritten
Glied der geometrischen Zahlenfolge wie 3 : 4. |
| Wie heißen
beide Zahlenfolgen bis zu 5. Glied? |
|
|
4 P |
|
|
Aufgabe 3b: |
| Eine
arithmetische und eine geometrische Zahlenfolge
haben dasselbe Anfangsglied 8 und stimmen auch im
zweiten Glied überein. Das dritte Glied der
arithmetischen Zahlenfolge verhält sich zum dritten
Glied der geometrischen Zahlenfolge wie 3 : 4. |
| Berechne die
Summen der ersten 10 Glieder beider Zahlenfolgen! |
|
|
4 P |
|
|
Aufgabe 3c: |
| Eine
arithmetische und eine geometrische Zahlenfolge
haben dasselbe Anfangsglied 8 und stimmen auch im
zweiten Glied überein. Das dritte Glied der
arithmetischen Zahlenfolge verhält sich zum dritten
Glied der geometrischen Zahlenfolge wie 3 : 4. |
| Wie groß sind
die 15. Glieder beider Zahlenfolgen? |
|
|
3 P |
|
|
Aufgabe 4a: |
Das Volumen eines quadratischen Pyramidenstumpfes mit der
Höhe  beträgt
beträgt  .
Das Produkt der Maßzahlen aus der Grundkante a und der
Deckkante b ist 16. .
Das Produkt der Maßzahlen aus der Grundkante a und der
Deckkante b ist 16. |
|
Berechne die Grundkante a und die Deckkante b! |
|
4 P |
|
|
Aufgabe 4b: |
Das Volumen eines quadratischen Pyramidenstumpfes mit der
Höhe  beträgt
beträgt  .
Das Produkt der Maßzahlen aus der Grundkante a und der
Deckkante b ist 16. .
Das Produkt der Maßzahlen aus der Grundkante a und der
Deckkante b ist 16. |
Berechne die Seitenhöhe
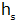 ! ! |
|
3 P |
|
|
Aufgabe 4c: |
Das Volumen eines quadratischen Pyramidenstumpfes mit der
Höhe  beträgt
beträgt  .
Das Produkt der Maßzahlen aus der Grundkante a und der
Deckkante b ist 16. .
Das Produkt der Maßzahlen aus der Grundkante a und der
Deckkante b ist 16. |
|
Wie groß ist die Mantelfläche? |
|
2 P |
|
|
Aufgabe 4d: |
Das Volumen eines quadratischen Pyramidenstumpfes mit der
Höhe  beträgt
beträgt  .
Das Produkt der Maßzahlen aus der Grundkante a und der
Deckkante b ist 16. .
Das Produkt der Maßzahlen aus der Grundkante a und der
Deckkante b ist 16. |
Wie groß ist der Winkel
 zwischen Seitenhöhe und Körperhöhe?
zwischen Seitenhöhe und Körperhöhe? |
|
2 P |
|
|
Aufgabe 5a: |
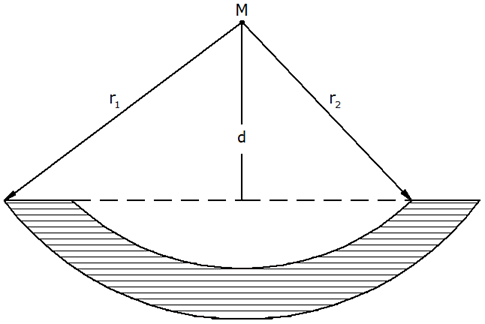
| Nebenstehende Skizze zeigt einen
Hohlkugelabschnitt mit folgenden Maßen: |
|
|
| Zeichne einen Achsenschnitt im Maßstab 1
: 5! |
|
 |
|
|
4 P |
|
|
Aufgabe 5b: |
| Nebenstehende Skizze zeigt einen
Hohlkugelabschnitt mit folgenden Maßen: |
|
|
| Berechne die Radien des als
Schnittfläche entstehenden Kreisringes! |
|
 |
|
|
4 P |
|
|
Aufgabe 5c: |
| Nebenstehende Skizze zeigt einen
Hohlkugelabschnitt mit folgenden Maßen: |
|
|
| Wie groß sind Volumen und Oberfläche des
Schalensegmentes? |
|
 |
|
|
3 P |
|
|
Aufgabe 6a: |
| Gegeben sind
zwei Geraden |
 |
|
und |
 . . |
|
Bestimme graphisch den Schnittpunkt S beider
Geraden! |
|
|
4 P |
|
|
Aufgabe 6b: |
| Gegeben sind
zwei Geraden |
 |
|
und |
 . . |
|
Berechne die Koordinaten von S! |
|
|
4 P |
|
|
Aufgabe 6c: |
|
Gegeben sind zwei Geraden |
 |
|
und |
 . . |
|
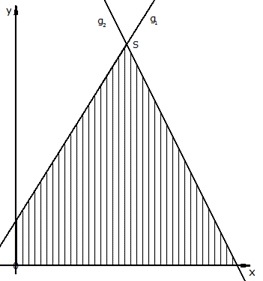
Die in nebenstehender Skizze schraffierte Fläche
wird um die y-Achse gedreht. |
|
Welches Volumen hat der entstehende Rotationskörper? |
|
|
 |
3 P |
|
|
Aufgabe 7a: |
Der Punkt
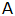 liegt
liegt
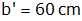 und der Punkt
und der Punkt
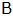 liegt
liegt
 vor einer Spiegelebene
vor einer Spiegelebene
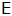 . . |
Ein von
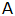 ausgehender Lichtstrahl, der mit
ausgehender Lichtstrahl, der mit
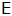 den Winkel
den Winkel
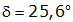 bildet, wird im Punkt
bildet, wird im Punkt
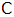 |
nach
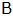 zurückgeworfen.
zurückgeworfen. |
|
Fertige eine Zeichnung im Maßstab 1 : 20 an! |
|
|
4 P |
|
|
Aufgabe 7b: |
Der Punkt
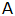 liegt
liegt
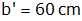 und der Punkt
und der Punkt
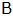 liegt
liegt
 vor einer Spiegelebene
vor einer Spiegelebene
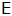 . . |
Ein von
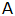 ausgehender Lichtstrahl, der mit
ausgehender Lichtstrahl, der mit
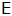 den Winkel
den Winkel
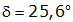 bildet, wird im Punkt
bildet, wird im Punkt
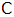 |
nach
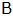 zurückgeworfen.
zurückgeworfen. |
Wie weit sind
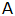 und
und
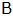 voneinander entfernt?
voneinander entfernt? |
|
|
4 P |
|
|
Aufgabe 7c: |
Der Punkt
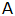 liegt
liegt
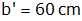 und der Punkt
und der Punkt
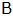 liegt
liegt
 vor einer Spiegelebene
vor einer Spiegelebene
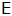 . . |
Ein von
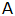 ausgehender Lichtstrahl, der mit
ausgehender Lichtstrahl, der mit
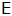 den Winkel
den Winkel
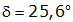 bildet, wird im Punkt
bildet, wird im Punkt
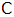 |
nach
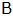 zurückgeworfen.
zurückgeworfen. |
Welche Winkel
 bildet
bildet
 mit dem einfallenden und mit dem
ausfallenden Strahl?
mit dem einfallenden und mit dem
ausfallenden Strahl? |
|
|
3 P |
|
|
Aufgabe 8a: |
Nach nebenstehender Skizze ergibt sich
die Strecke y durch Konstruktion aus den
Größen a und
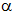 . . |
Drücke alle Winkel in Abhängigkeit von
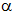 aus und stelle y als Funktion von a und
aus und stelle y als Funktion von a und
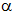 dar!
dar! |
|
 |
|
|
4 P |
|
|
Aufgabe 8b: |
Nach nebenstehender Skizze ergibt sich
die Strecke y durch Konstruktion aus den
Größen a und
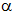 . . |
Berechne den Funktionswert für
 und
und
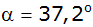 ! ! |
|
 |
|
|
4 P |
|
|
Aufgabe 8c: |
Nach nebenstehender Skizze ergibt sich
die Strecke y durch Konstruktion aus den
Größen a und
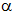 . . |
Welchen Wert nimmt y für
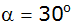 an?
an? |
|
 |
|
|
3 P |
|