|
Aufgabe 1a: |
| Jemand spielt
im Lotto mit 20 DM Einsatz. Er hat Pech und setzt
das nächste Mal 22 DM, dann 24 DM usw. Plötzlich hat
er Glück und gewinnt sein bisher verwettetes Geld
auf einmal zurück. |
|
Beim wievielten Spiel ist das der Fall, wenn sein
Gewinn das Fünffache des letzten Einsatzes betrug? |
|
|
4 P |
|
|
Aufgabe 1b: |
| Jemand spielt
im Lotto mit 20 DM Einsatz. Er hat Pech und setzt
das nächste Mal 22 DM, dann 24 DM usw. Plötzlich hat
er Glück und gewinnt sein bisher verwettetes Geld
auf einmal zurück. |
|
Wie hoch waren bei diesem Spiel sein Einsatz und
sein Gewinn? |
|
|
4 P |
|
|
Aufgabe 1c: |
| Jemand spielt
im Lotto mit 20 DM Einsatz. Er hat Pech und setzt
das nächste Mal 22 DM, dann 24 DM usw. Plötzlich hat
er Glück und gewinnt sein bisher verwettetes Geld
auf einmal zurück. |
|
Stelle eine Tabelle des Spielverlaufes auf! |
|
|
3 P |
|
|
Aufgabe 2a: |
Einem Quadrat
mit der Seite
 ist ein Kreis, diesem Kreis wieder ein Quadrat usw.
einbeschrieben. Auf diese Weise entsteht eine Folge
einander einbeschriebener Kreise und Quadrate.
ist ein Kreis, diesem Kreis wieder ein Quadrat usw.
einbeschrieben. Auf diese Weise entsteht eine Folge
einander einbeschriebener Kreise und Quadrate. |
Fertige eine Zeichnung im Maßstab 1 : 3 bis zum
Quadrat
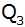 an!
an! |
|
|
1 P |
|
|
Aufgabe 2b: |
Einem Quadrat
mit der Seite
 ist ein Kreis, diesem Kreis wieder ein Quadrat usw.
einbeschrieben. Auf diese Weise entsteht eine Folge
einander einbeschriebener Kreise und Quadrate.
ist ein Kreis, diesem Kreis wieder ein Quadrat usw.
einbeschrieben. Auf diese Weise entsteht eine Folge
einander einbeschriebener Kreise und Quadrate. |
|
Berechne die Differenz zwischen der Fläche des 7.
Quadrates und der Fläche des 7. Kreises! |
|
|
2 P |
|
|
Aufgabe 2c: |
Einem Quadrat
mit der Seite
 ist ein Kreis, diesem Kreis wieder ein Quadrat usw.
einbeschrieben. Auf diese Weise entsteht eine Folge
einander einbeschriebener Kreise und Quadrate.
ist ein Kreis, diesem Kreis wieder ein Quadrat usw.
einbeschrieben. Auf diese Weise entsteht eine Folge
einander einbeschriebener Kreise und Quadrate. |
|
Berechne die Summe der Flächen der ersten 7
Quadrate! |
|
|
2 P |
|
|
Aufgabe 2d: |
Einem Quadrat
mit der Seite
 ist ein Kreis, diesem Kreis wieder ein Quadrat usw.
einbeschrieben. Auf diese Weise entsteht eine Folge
einander einbeschriebener Kreise und Quadrate.
ist ein Kreis, diesem Kreis wieder ein Quadrat usw.
einbeschrieben. Auf diese Weise entsteht eine Folge
einander einbeschriebener Kreise und Quadrate. |
Das wievielte Quadrat hat zum ersten Mal eine
kleinere Fläche als
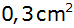 ? ? |
|
|
2 P |
|
|
Aufgabe 3a: |
Ein Kapital
 wird zu
wird zu
 Prozent verzinst. Die Zinsen werden am Ende eines
jeden Jahres zum Kapital geschlagen und in der Folge
mitverzinst.
Prozent verzinst. Die Zinsen werden am Ende eines
jeden Jahres zum Kapital geschlagen und in der Folge
mitverzinst. |
|
Wie groß ist das Kapital am Ende des ersten, des
zweiten, des dritten, des n-ten Jahres? |
|
|
4 P |
|
|
Aufgabe 3b: |
Ein Kapital
 wird zu
wird zu
 Prozent verzinst. Die Zinsen werden am Ende eines
jeden Jahres zum Kapital geschlagen und in der Folge
mitverzinst.
Prozent verzinst. Die Zinsen werden am Ende eines
jeden Jahres zum Kapital geschlagen und in der Folge
mitverzinst. |
|
Nach wieviel Jahren hat sich das Kapital
verdreifacht, das zu 8% ausgeliehen war? |
|
|
4 P |
|
|
Aufgabe 3c: |
Ein Kapital
 wird zu
wird zu
 Prozent verzinst. Die Zinsen werden am Ende eines
jeden Jahres zum Kapital geschlagen und in der Folge
mitverzinst.
Prozent verzinst. Die Zinsen werden am Ende eines
jeden Jahres zum Kapital geschlagen und in der Folge
mitverzinst. |
|
Zu welchem Zinsfuß war ein Kapital ausgeliehen, das
sich in 15 Jahren verdoppelte? |
|
|
3 P |
|
|
Aufgabe 4a: |
Ein behauener
Stein hat die Form eines sich nach oben verjüngenden
quadratischen Pyramidenstumpfes mit der Deckkante
 ,
der Seitenflächenhöhe ,
der Seitenflächenhöhe
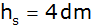 und der Seitenkante
und der Seitenkante
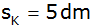 .
Aus diesem Stein .
Aus diesem Stein
ist ein kegelstumpfförmiges
Becken mit
 und
und
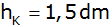 so herausgearbeitet worden, daß die Spitze des
Ergänzungskegels im Mittelpunkt der
Pyramidenstumpfgrundfläche liegen würde.
so herausgearbeitet worden, daß die Spitze des
Ergänzungskegels im Mittelpunkt der
Pyramidenstumpfgrundfläche liegen würde. |
Berechne die Grundkante
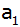 und die Höhe
und die Höhe
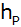 des Pyramidenstumpfes, sowie den Grundkreisradius
des Pyramidenstumpfes, sowie den Grundkreisradius
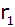 des Kegel- stumpfes!
des Kegel- stumpfes! |
|
|
4 P |
|
|
Aufgabe 4b: |
Ein behauener
Stein hat die Form eines sich nach oben verjüngenden
quadratischen Pyramidenstumpfes mit der Deckkante
 ,
der Seitenflächenhöhe ,
der Seitenflächenhöhe
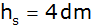 und der Seitenkante
und der Seitenkante
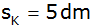 .
Aus diesem Stein .
Aus diesem Stein
ist ein kegelstumpfförmiges
Becken mit
 und
und
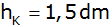 so herausgearbeitet worden, daß die Spitze des
Ergänzungskegels im Mittelpunkt der
Pyramidenstumpfgrundfläche liegen würde.
so herausgearbeitet worden, daß die Spitze des
Ergänzungskegels im Mittelpunkt der
Pyramidenstumpfgrundfläche liegen würde. |
|
Fertige eine Zeichnung als Parallelschnitt oder als
Diagonalschnitt im Maßstab 1 : 10 an! |
|
|
2 P |
|
|
Aufgabe 4c: |
Ein behauener
Stein hat die Form eines sich nach oben verjüngenden
quadratischen Pyramidenstumpfes mit der Deckkante
 ,
der Seitenflächenhöhe ,
der Seitenflächenhöhe
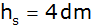 und der Seitenkante
und der Seitenkante
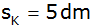 .
Aus diesem Stein .
Aus diesem Stein
ist ein kegelstumpfförmiges
Becken mit
 und
und
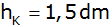 so herausgearbeitet worden, daß die Spitze des
Ergänzungskegels im Mittelpunkt der
Pyramidenstumpfgrundfläche liegen würde.
so herausgearbeitet worden, daß die Spitze des
Ergänzungskegels im Mittelpunkt der
Pyramidenstumpfgrundfläche liegen würde. |
|
Berechne das Volumen des Restkörpers! |
|
|
3 P |
|
|
Aufgabe 4d: |
Ein behauener
Stein hat die Form eines sich nach oben verjüngenden
quadratischen Pyramidenstumpfes mit der Deckkante
 ,
der Seitenflächenhöhe ,
der Seitenflächenhöhe
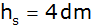 und der Seitenkante
und der Seitenkante
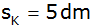 .
Aus diesem Stein .
Aus diesem Stein
ist ein kegelstumpfförmiges
Becken mit
 und
und
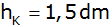 so herausgearbeitet worden, daß die Spitze des
Ergänzungskegels im Mittelpunkt der
Pyramidenstumpfgrundfläche liegen würde.
so herausgearbeitet worden, daß die Spitze des
Ergänzungskegels im Mittelpunkt der
Pyramidenstumpfgrundfläche liegen würde. |
|
Berechne die Mantelfläche des Kegelstumpfes! |
|
|
2 P |
|
|
Aufgabe 5a: |
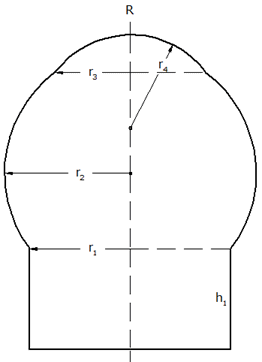
| Die nebenstehende Figur wird um ihre
Achse gedreht. |
|
Maße: |
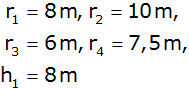 |
|
Konstruiere den Achsenschnitt des
Drehkörpers
im Maßstab 1 : 200! |
|
 |
|
|
5,5 P |
|
|
Aufgabe 5b: |
| Die nebenstehende Figur wird um ihre
Achse gedreht. |
|
Maße: |
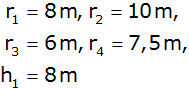 |
|
| Berechne das Volumen des Drehkörpers! |
|
 |
|
|
5,5 P |
|
|
Aufgabe 6a: |
Ein
ungleichseitiges Dreieck rotiert um seine Seite
 .
Der Winkel .
Der Winkel
 des Dreiecks beträgt
des Dreiecks beträgt
 ,
der ,
der
Winkel
 beträgt
beträgt
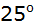 . . |
|
Zeichne einen Achsenschnitt des Rotationskörpers! |
|
|
4 P |
|
|
Aufgabe 6b: |
Ein
ungleichseitiges Dreieck rotiert um seine Seite
 .
Der Winkel .
Der Winkel
 des Dreiecks beträgt
des Dreiecks beträgt
 ,
der ,
der
Winkel
 beträgt
beträgt
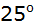 . . |
|
Berechne das Volumen des Rotationskörpers! |
|
|
4 P |
|
|
Aufgabe 6c: |
Ein
ungleichseitiges Dreieck rotiert um seine Seite
 .
Der Winkel .
Der Winkel
 des Dreiecks beträgt
des Dreiecks beträgt
 ,
der ,
der
Winkel
 beträgt
beträgt
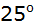 . . |
|
Berechne die Oberfläche des Rotationskörpers! |
|
|
4 P |
|
|
Aufgabe 7a: |
Gegeben sind
drei Kreise mit den Radien
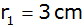 ; ;
 und
und
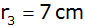 .
Jeder Kreis berührt die beiden anderen Kreise von
außen. .
Jeder Kreis berührt die beiden anderen Kreise von
außen. |
|
Zeichne die Figur! |
|
|
4 P |
|
|
Aufgabe 7b: |
Gegeben sind
drei Kreise mit den Radien
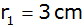 ; ;
 und
und
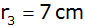 .
Jeder Kreis berührt die beiden anderen Kreise von
außen. .
Jeder Kreis berührt die beiden anderen Kreise von
außen. |
Welche Winkel bilden die Verbindungsgeraden der
Kreismittelpunkte
 , ,
 und
und
 miteinander?
miteinander? |
|
|
4 P |
|
|
Aufgabe 7c: |
Gegeben sind
drei Kreise mit den Radien
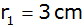 ; ;
 und
und
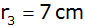 .
Jeder Kreis berührt die beiden anderen Kreise von
außen. .
Jeder Kreis berührt die beiden anderen Kreise von
außen. |
Berechne die Fläche des Dreiecks
 ! ! |
|
|
3 P |
|
|
Aufgabe 8a: |
| Zeichne ein
(spitzwinkliges) Dreieck mit Umkreis! |
Zeige, daß darin
 ist!
ist! |
|
|
2 P |
|
|
Aufgabe 8b: |
Von einem
Dreieck sind die Seiten
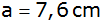 und
und
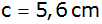 sowie der Umkreisradius
sowie der Umkreisradius
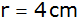 gegeben.
gegeben. |
Berechne die Dreieckswinkel und die Dreiecksseite
 ! ! |
|
|
3 P |
|
|
Aufgabe 8c: |
Von einem
Dreieck sind die Seiten
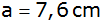 und
und
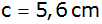 sowie der Umkreisradius
sowie der Umkreisradius
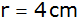 gegeben.
gegeben. |
|
Zeichne das Dreieck! |
|
|
3 P |
|
|
Aufgabe 8d: |
Von einem
Dreieck sind die Seiten
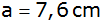 und
und
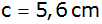 sowie der Umkreisradius
sowie der Umkreisradius
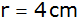 gegeben.
gegeben. |
|
Berechne für dieses Dreieck die Differenz zwischen
Kreisfläche und Dreiecksfläche! |
|
|
3 P |
|