|
Aufgabe 1a: |
| Eine Schuld von
150000 DM soll in der Weise abgetragen werden, daß
jedes Jahr die Rückzahlung um den gleichen Betrag
erhöht wird. Im 4. Jahr beträgt die Rückzahlung 6000
DM, im 10. Jahr doppelt so viel. |
|
Welche Summe musste im ersten Jahr gezahlt werden? |
|
|
4 P |
|
|
Aufgabe 1b: |
| Eine Schuld von
150000 DM soll in der Weise abgetragen werden, daß
jedes Jahr die Rückzahlung um den gleichen Betrag
erhöht wird. Im 4. Jahr beträgt die Rückzahlung 6000
DM, im 10. Jahr doppelt so viel. |
|
Wieviel Jahre dauert die Rückzahlung? |
|
|
4 P |
|
|
Aufgabe 1c: |
| Eine Schuld von
150000 DM soll in der Weise abgetragen werden, daß
jedes Jahr die Rückzahlung um den gleichen Betrag
erhöht wird. Im 4. Jahr beträgt die Rückzahlung 6000
DM, im 10. Jahr doppelt so viel. |
|
Welche Summe muß im letzten Jahr gezahlt werden? |
|
|
3 P |
|
|
Aufgabe 2a: |
Ein Pendel
schwingt bis zu den Umkehrpunkten
 , ,
 , ,
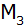 , ,
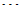 ,
denen die seitlichen Abstände ,
denen die seitlichen Abstände
 , ,
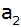 , ,
 , ,
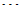 (gemessen vom Lot durch den Aufhängepunkt)
entsprechen.
(gemessen vom Lot durch den Aufhängepunkt)
entsprechen. |
|
Die seitlichen Abstände sind wegen der auftretenden
Reibungskräfte jeweils 0,1 kleiner als die
unmittelbar vorhergegangenen. |
|
Fertige eine Skizze an! |
|
|
4 P |
|
|
Aufgabe 2b: |
Ein Pendel
schwingt bis zu den Umkehrpunkten
 , ,
 , ,
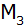 , ,
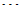 ,
denen die seitlichen Abstände ,
denen die seitlichen Abstände
 , ,
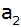 , ,
 , ,
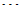 (gemessen vom Lot durch den Aufhängepunkt)
entsprechen.
(gemessen vom Lot durch den Aufhängepunkt)
entsprechen. |
|
Die seitlichen Abstände sind wegen der auftretenden
Reibungskräfte jeweils 0,1 kleiner als die
unmittelbar vorhergegangenen. |
Wie groß ist der Abstand
 ,
wenn ,
wenn
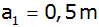 ist?
ist? |
|
|
4 P |
|
|
Aufgabe 2c: |
Ein Pendel
schwingt bis zu den Umkehrpunkten
 , ,
 , ,
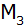 , ,
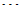 ,
denen die seitlichen Abstände ,
denen die seitlichen Abstände
 , ,
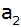 , ,
 , ,
 (gemessen vom Lot durch den Aufhängepunkt)
entsprechen.
(gemessen vom Lot durch den Aufhängepunkt)
entsprechen. |
|
Die seitlichen Abstände sind wegen der auftretenden
Reibungskräfte jeweils 0,1 kleiner als die
unmittelbar vorhergegangenen. |
|
In welchem Umkehrpunkt ist der seitliche Abstand zum
ersten Male kleiner als 1 cm? |
|
|
3 P |
|
|
Aufgabe 3a: |
| Ein Vater legte
am Ende des Geburtsjahres seiner Tochter 1000 DM, in
den folgenden 4 Jahren jeweils 1000 DM mehr als in
dem vorangegangenen Jahr auf einem Sparkonto an. Ein
anderer Vater legte am Ende des Geburtsjahres seines
Sohnes 5000 DM, in den folgenden 4 Jahren jeweils
1000 DM weniger als in dem vorangegangenen Jahr auf
einem Sparkonto an. Alle Spareinlagen wurden mit 5%
verzinst. |
|
Welcher Betrag stand der Tochter 21 Jahre nach der
ersten Einzahlung als Mitgift zur Verfügung? |
|
|
4 P |
|
|
Aufgabe 3b: |
| Ein Vater legte
am Ende des Geburtsjahres seiner Tochter 1000 DM, in
den folgenden 4 Jahren jeweils 1000 DM mehr als in
dem vorangegangenen Jahr auf einem Sparkonto an. Ein
anderer Vater legte am Ende des Geburtsjahres seines
Sohnes 5000 DM, in den folgenden 4 Jahren jeweils
1000 DM weniger als in dem vorangegangenen Jahr auf
einem Sparkonto an. Alle Spareinlagen wurden mit 5%
verzinst. |
|
Welcher Betrag stand dem Sohn 18 Jahre nach der
ersten Einzahlung für sein Studium zur Verfügung? |
|
|
4 P |
|
|
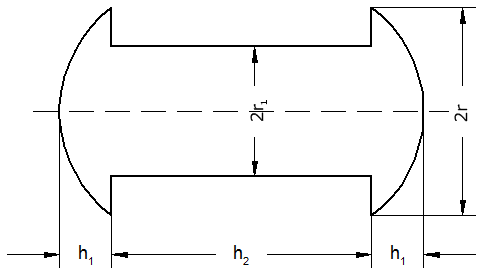
Aufgabe 4a: |
Nebenstehende Skizze stellt den
Achsenschnitt eines Werkstoffes aus Holz (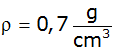 )
dar, das aus einem Zylinder mit dem Radius )
dar, das aus einem Zylinder mit dem Radius
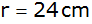 und der Höhe
und der Höhe
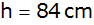 herausgedreht wurde.
herausgedreht wurde. |
Weitere Maße sind:
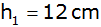 , ,
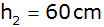 und
und
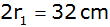 . . |
Berechne den Radius
 der den Kugelabschnitten zugehörigen Kugeln!
der den Kugelabschnitten zugehörigen Kugeln! |
|
 |
|
|
3 P |
|
|
Aufgabe 4b: |
Nebenstehende Skizze stellt den
Achsenschnitt eines Werkstoffes aus Holz (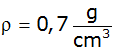 )
dar, das aus einem Zylinder mit dem Radius )
dar, das aus einem Zylinder mit dem Radius
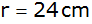 und der Höhe
und der Höhe
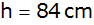 herausgedreht wurde.
herausgedreht wurde. |
Weitere Maße sind:
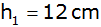 , ,
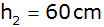 und
und
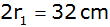 . . |
| Fertige eine
Zeichnung im Maßstab 1 : 12 an! |
|
 |
|
|
2 P |
|
|
Aufgabe 4c: |
Nebenstehende Skizze stellt den
Achsenschnitt eines Werkstoffes aus Holz (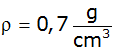 )
dar, das aus einem Zylinder mit dem Radius )
dar, das aus einem Zylinder mit dem Radius
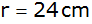 und der Höhe
und der Höhe
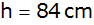 herausgedreht wurde.
herausgedreht wurde. |
Weitere Maße sind:
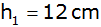 , ,
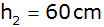 und
und
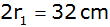 . . |
| Welche Masse hat das
Werkstück? |
|
 |
|
|
3 P |
|
|
Aufgabe 4d: |
Nebenstehende Skizze stellt den
Achsenschnitt eines Werkstoffes aus Holz (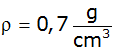 )
dar, das aus einem Zylinder mit dem Radius )
dar, das aus einem Zylinder mit dem Radius
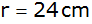 und der Höhe
und der Höhe
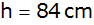 herausgedreht wurde.
herausgedreht wurde. |
Weitere Maße sind:
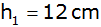 , ,
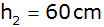 und
und
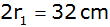 . . |
|
Wieviel Prozent des ursprünglichen Zylinders
beträgt der Abfall? |
|
 |
|
|
3 P |
|
|
Aufgabe 5a: |
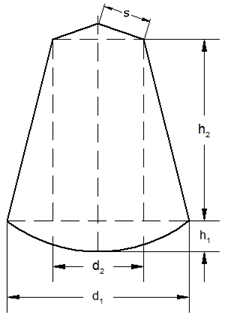
| Eine Raumkapsel hat den nebenstehenden
Achsenschnitt. |
|
Die Maße sind: |
|
|
|
Berechne die Fläche des Hitzeschildes! |
|
 |
|
|
4 P |
|
|
Aufgabe 5b: |
| Eine Raumkapsel hat den nebenstehenden
Achsenschnitt. |
|
Die Maße sind: |
|
|
|
Welches Volumen hat die Raumkapsel? |
|
 |
|
|
4 P |
|
|
Aufgabe 5c: |
| Eine Raumkapsel hat den nebenstehenden
Achsenschnitt. |
|
Die Maße sind: |
|
|
|
Zeichne einen Achsenschnitt im Maßstab 1 :
100! |
|
 |
|
|
3 P |
|
|
Aufgabe 6a: |
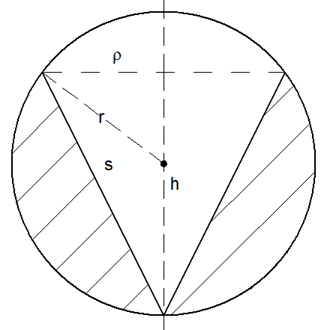
Aus einer Kugel wurde ein Kegel mit dem
Radius
 so herausgedreht, daß die Kegelachse durch
den Kugelmittelpunkt geht und die
Kegelspitze in der Kugeloberfläche liegt
(siehe nebenstehende Skizze).
so herausgedreht, daß die Kegelachse durch
den Kugelmittelpunkt geht und die
Kegelspitze in der Kugeloberfläche liegt
(siehe nebenstehende Skizze). |
|
Die Höhe des Kegels ist gleich seinem
Grundkreisdurchmesser. |
|
Zeichne einen Achsenschnitt im Maßstab 1 :
6! |
|
 |
|
|
3 P |
|
|
Aufgabe 6b: |
Aus einer Kugel wurde ein Kegel mit dem
Radius
 so herausgedreht, daß die Kegelachse durch
den Kugelmittelpunkt geht und die
Kegelspitze in der Kugeloberfläche liegt
(siehe nebenstehende Skizze).
so herausgedreht, daß die Kegelachse durch
den Kugelmittelpunkt geht und die
Kegelspitze in der Kugeloberfläche liegt
(siehe nebenstehende Skizze). |
|
Die Höhe des Kegels ist gleich seinem
Grundkreisdurchmesser. |
Berechne die Kegelhöhe
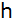 ,
die Kegelmantellinie ,
die Kegelmantellinie
 und den Kegelradius
und den Kegelradius
 ! ! |
|
 |
|
|
4 P |
|
|
Aufgabe 6c: |
Aus einer Kugel wurde ein Kegel mit dem
Radius
 so herausgedreht, daß die Kegelachse durch
den Kugelmittelpunkt geht und die
Kegelspitze in der Kugeloberfläche liegt
(siehe nebenstehende Skizze).
so herausgedreht, daß die Kegelachse durch
den Kugelmittelpunkt geht und die
Kegelspitze in der Kugeloberfläche liegt
(siehe nebenstehende Skizze). |
|
Die Höhe des Kegels ist gleich seinem
Grundkreisdurchmesser. |
|
Wie groß ist das Volumen des (gestrichelt
gezeichneten) Restkörpers? |
|
 |
|
|
4 P |
|
|
Aufgabe 7a: |
Ein
Fesselballon steht
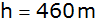 über der Erde. Von oben werden Fußpunkt und Spitze
eines Turmes unter
über der Erde. Von oben werden Fußpunkt und Spitze
eines Turmes unter
den Tiefenwinkeln
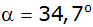 und
und
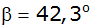 anvisiert.
anvisiert. |
Wie hoch (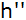 )
ist der Turm? )
ist der Turm? |
|
|
4 P |
|
|
Aufgabe 7b: |
Ein
Fesselballon steht
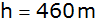 über der Erde. Von oben werden Fußpunkt und Spitze
eines Turmes unter
über der Erde. Von oben werden Fußpunkt und Spitze
eines Turmes unter
den Tiefenwinkeln
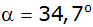 und
und
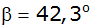 anvisiert.
anvisiert. |
|
Wie groß ist der Abstand (a) von der Turmspitze bis
zum Fesselballon? |
|
|
4 P |
|
|
Aufgabe 7c: |
Ein
Fesselballon steht
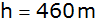 über der Erde. Von oben werden Fußpunkt und Spitze
eines Turmes unter
über der Erde. Von oben werden Fußpunkt und Spitze
eines Turmes unter
den Tiefenwinkeln
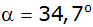 und
und
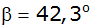 anvisiert.
anvisiert. |
Der Ballon steigt senkrecht um
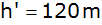 .
Wie groß ist jetzt der Abstand ( .
Wie groß ist jetzt der Abstand (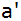 )
von der Turmspitze bis zum Fesselballon? )
von der Turmspitze bis zum Fesselballon? |
|
|
3 P |
|
|
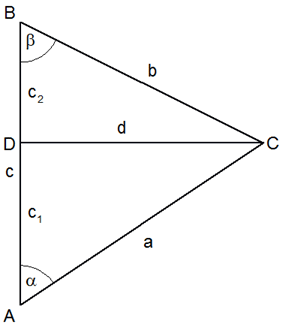
Aufgabe 8a: |
Vom Punkt
 einer geradlinigen Landstraße zweigt ein Weg
unter dem Winkel
einer geradlinigen Landstraße zweigt ein Weg
unter dem Winkel
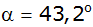 zu einem Bauernhof
zu einem Bauernhof
 ab.
ab. |
Ein Stück weiter führt ein zweiter Weg von
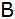 aus unter dem Winkel
aus unter dem Winkel
 zu dem Bauernhof
zu dem Bauernhof
 zurück.
zurück. |
Beide Wege begrenzen mit der Landstraße eine
Fläche von
 . . |
Berechne die Längen der Strecken
 , ,
 und
und
 ! ! |
|
 |
|
|
4 P |
|
|
Aufgabe 8b: |
Vom Punkt
 einer geradlinigen Landstraße zweigt ein Weg
unter dem Winkel
einer geradlinigen Landstraße zweigt ein Weg
unter dem Winkel
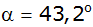 zu einem Bauernhof
zu einem Bauernhof
 ab.
ab. |
Ein Stück weiter führt ein zweiter Weg von
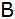 aus unter dem Winkel
aus unter dem Winkel
 zu dem Bauernhof
zu dem Bauernhof
 zurück.
zurück. |
Beide Wege begrenzen mit der Landstraße eine
Fläche von
 . . |
Wie lang ist der Fußweg
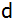 ,
der in ,
der in
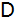 senkrecht auf die Landstraße führt?
senkrecht auf die Landstraße führt? |
|
 |
|
|
3 P |
|
|
Aufgabe 8c: |
Vom Punkt
 einer geradlinigen Landstraße zweigt ein Weg
unter dem Winkel
einer geradlinigen Landstraße zweigt ein Weg
unter dem Winkel
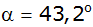 zu einem Bauernhof
zu einem Bauernhof
 ab.
ab. |
Ein Stück weiter führt ein zweiter Weg von
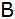 aus unter dem Winkel
aus unter dem Winkel
 zu dem Bauernhof
zu dem Bauernhof
 zurück.
zurück. |
Beide Wege begrenzen mit der Landstraße eine
Fläche von
 . . |
Berechne die Entfernungen
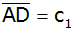 und
und
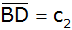 ! ! |
|
 |
|
|
2 P |
|
|
Aufgabe 8d: |
Vom Punkt
 einer geradlinigen Landstraße zweigt ein Weg
unter dem Winkel
einer geradlinigen Landstraße zweigt ein Weg
unter dem Winkel
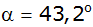 zu einem Bauernhof
zu einem Bauernhof
 ab.
ab. |
Ein Stück weiter führt ein zweiter Weg von
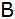 aus unter dem Winkel
aus unter dem Winkel
 zu dem Bauernhof
zu dem Bauernhof
 zurück.
zurück. |
Beide Wege begrenzen mit der Landstraße eine
Fläche von
 . . |
|
Fertige eine maßstabgerechte Zeichnung an! |
|
 |
|
|
2 P |
|