|
Aufgabe 1a: |
| Eine Stadt
plant eine Sportstätte. In der ersten Reihe des
Stadions befinden sich 886 Plätze. |
|
In jeder folgenden Reihe sollen 12 Plätze mehr als
in der vorhergehenden zur Verfügung stehen. |
|
Wieviel Plätze befinden sich in der 12. Reihe? |
|
|
4 P |
|
|
Aufgabe 1b: |
| Eine Stadt
plant eine Sportstätte. In der ersten Reihe des
Stadions befinden sich 886 Plätze. |
|
In jeder folgenden Reihe sollen 12 Plätze mehr als
in der vorhergehenden zur Verfügung stehen. |
|
Wieviel Plätze stehen in 12 Reihen insgesamt zur
Verfügung? |
|
|
4 P |
|
|
Aufgabe 1c: |
| Eine Stadt
plant eine Sportstätte. In der ersten Reihe des
Stadions befinden sich 886 Plätze. |
|
In jeder folgenden Reihe sollen 12 Plätze mehr als
in der vorhergehenden zur Verfügung stehen. |
|
Wieviel Sitzreihen sind zu bauen, wenn 20000
Personen einen Sitzplatz finden sollen? |
|
|
3 P |
|
|
Aufgabe 2a: |
Die Geraden
 und
und
 schneiden einander im Punkt
schneiden einander im Punkt
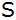 unter dem Winkel
unter dem Winkel
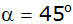 .
In einem Punkt .
In einem Punkt
 der ersten Geraden, der
der ersten Geraden, der
 von
von
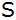 entfernt liegt, wird die Senkrechte
entfernt liegt, wird die Senkrechte
 errichtet. Sie schneidet die zweite Gerade im Punkt
errichtet. Sie schneidet die zweite Gerade im Punkt
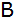 .
In .
In
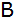 wird nun auf der zweiten Geraden die Senkrechte
wird nun auf der zweiten Geraden die Senkrechte
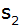 errichtet und der Schnittpunkt
errichtet und der Schnittpunkt
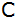 mit der ersten Geraden usw. bestimmt.
mit der ersten Geraden usw. bestimmt. |
Fertige eine Zeichnung im Maßstab 1 : 2 bis zur
Senkrechten
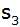 an!
an! |
|
|
2 P |
|
|
Aufgabe 2b: |
Die Geraden
 und
und
 schneiden einander im Punkt
schneiden einander im Punkt
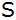 unter dem Winkel
unter dem Winkel
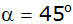 .
In einem Punkt .
In einem Punkt
 der ersten Geraden, der
der ersten Geraden, der
 von
von
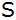 entfernt liegt, wird die Senkrechte
entfernt liegt, wird die Senkrechte
 errichtet. Sie schneidet die zweite Gerade im Punkt
errichtet. Sie schneidet die zweite Gerade im Punkt
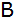 .
In .
In
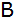 wird nun auf der zweiten Geraden die Senkrechte
wird nun auf der zweiten Geraden die Senkrechte
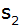 errichtet und der Schnittpunkt
errichtet und der Schnittpunkt
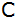 mit der ersten Geraden usw. bestimmt.
mit der ersten Geraden usw. bestimmt. |
|
Berechne die Gesamtlänge der ersten 14 Senkrechten! |
|
|
3 P |
|
|
Aufgabe 2c: |
Die Geraden
 und
und
 schneiden einander im Punkt
schneiden einander im Punkt
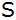 unter dem Winkel
unter dem Winkel
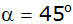 .
In einem Punkt .
In einem Punkt
 der ersten Geraden, der
der ersten Geraden, der
 von
von
 entfernt liegt, wird die Senkrechte
entfernt liegt, wird die Senkrechte
 errichtet. Sie schneidet die zweite Gerade im Punkt
errichtet. Sie schneidet die zweite Gerade im Punkt
 .
In .
In
 wird nun auf der zweiten Geraden die Senkrechte
wird nun auf der zweiten Geraden die Senkrechte
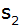 errichtet und der Schnittpunkt
errichtet und der Schnittpunkt
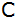 mit der ersten Geraden usw. bestimmt.
mit der ersten Geraden usw. bestimmt. |
|
Welche Länge hat die 11. Senkrechte? |
|
|
3 P |
|
|
Aufgabe 2d: |
Die Geraden
 und
und
 schneiden einander im Punkt
schneiden einander im Punkt
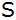 unter dem Winkel
unter dem Winkel
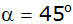 .
In einem Punkt .
In einem Punkt
 der ersten Geraden, der
der ersten Geraden, der
 von
von
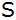 entfernt liegt, wird die Senkrechte
entfernt liegt, wird die Senkrechte
 errichtet. Sie schneidet die zweite Gerade im Punkt
errichtet. Sie schneidet die zweite Gerade im Punkt
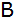 .
In .
In
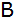 wird nun auf der zweiten Geraden die Senkrechte
wird nun auf der zweiten Geraden die Senkrechte
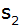 errichtet und der Schnittpunkt
errichtet und der Schnittpunkt
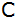 mit der ersten Geraden usw. bestimmt.
mit der ersten Geraden usw. bestimmt. |
|
Die wievielte Senkrechte ist zum ersten Male länger
als 42 cm? |
|
|
3 P |
|
|
Aufgabe 3a: |
Aus einer
bestimmten Entfernung erscheint die Spitze eines
Fernsehturmes unter dem Höhenwinkel
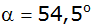 . . |
Tritt man
 zurück, so beträgt der Höhenwinkel nur noch
zurück, so beträgt der Höhenwinkel nur noch
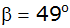 . . |
Die Augenhöhe des Beobachters, der sich in der
gleichen Horizontalebene wie der Fernsehturm
befindet, beträgt
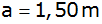 . . |
|
Fertige eine Skizze an! |
|
|
2 P |
|
|
Aufgabe 3b: |
Aus einer
bestimmten Entfernung erscheint die Spitze eines
Fernsehturmes unter dem Höhenwinkel
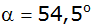 . . |
Tritt man
 zurück, so beträgt der Höhenwinkel nur noch
zurück, so beträgt der Höhenwinkel nur noch
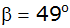 . . |
Die Augenhöhe des Beobachters, der sich in der
gleichen Horizontalebene wie der Fernsehturm
befindet, beträgt
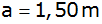 . . |
Wie hoch (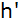 )
ist der Turm? )
ist der Turm? |
|
|
3 P |
|
|
Aufgabe 3c: |
Aus einer
bestimmten Entfernung erscheint die Spitze eines
Fernsehturmes unter dem Höhenwinkel
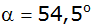 . . |
Tritt man
 zurück, so beträgt der Höhenwinkel nur noch
zurück, so beträgt der Höhenwinkel nur noch
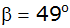 . . |
Die Augenhöhe des Beobachters, der sich in der
gleichen Horizontalebene wie der Fernsehturm
befindet, beträgt
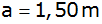 . . |
Wie weit (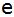 )
war der Beobachter bei der ersten Messung vom Fuß
des Turmes entfernt? )
war der Beobachter bei der ersten Messung vom Fuß
des Turmes entfernt? |
|
|
3 P |
|
|
Aufgabe 3d: |
Aus einer
bestimmten Entfernung erscheint die Spitze eines
Fernsehturmes unter dem Höhenwinkel
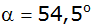 . . |
Tritt man
 zurück, so beträgt der Höhenwinkel nur noch
zurück, so beträgt der Höhenwinkel nur noch
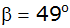 . . |
Die Augenhöhe des Beobachters, der sich in der
gleichen Horizontalebene wie der Fernsehturm
befindet, beträgt
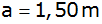 . . |
Das Ufer eines Sees liegt
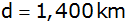 vom Fuß des Turmes entfernt.
vom Fuß des Turmes entfernt. |
Unter welchem Tiefenwinkel (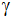 )
erscheint das Seeufer von der )
erscheint das Seeufer von der
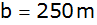 hohen Aussichtsplattform des Turmes?
hohen Aussichtsplattform des Turmes? |
|
|
3 P |
|
|
Aufgabe 4a: |
Ein Berghotel
liegt
 über dem Wasserspiegel eines Sees.
über dem Wasserspiegel eines Sees. |
Vom Hotel aus erblickt ein Beobachter einen
Wetterballon unter dem Höhenwinkel
 ,
dessen Spiegelbild im See unter dem Tiefenwinkel ,
dessen Spiegelbild im See unter dem Tiefenwinkel
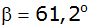 . . |
|
Fertige eine Skizze an! |
|
|
2 P |
|
|
Aufgabe 4b: |
Ein Berghotel
liegt
 über dem Wasserspiegel eines Sees.
über dem Wasserspiegel eines Sees. |
Vom Hotel aus erblickt ein Beobachter einen
Wetterballon unter dem Höhenwinkel
 ,
dessen Spiegelbild im See unter dem Tiefenwinkel ,
dessen Spiegelbild im See unter dem Tiefenwinkel
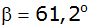 . . |
Wie hoch (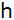 )
stand der Ballon über dem See? )
stand der Ballon über dem See? |
|
|
3 P |
|
|
Aufgabe 4c: |
Ein Berghotel
liegt
 über dem Wasserspiegel eines Sees.
über dem Wasserspiegel eines Sees. |
Vom Hotel aus erblickt ein Beobachter einen
Wetterballon unter dem Höhenwinkel
 ,
dessen Spiegelbild im See unter dem Tiefenwinkel ,
dessen Spiegelbild im See unter dem Tiefenwinkel
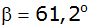 . . |
Wie weit ( )
war der Ballon vom Beobachter entfernt? )
war der Ballon vom Beobachter entfernt? |
|
|
3 P |
|
|
Aufgabe 5a: |
Der Pilot eines
Sportflugzeuges sieht das Licht an der Spitze eines
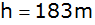 hohen Sendemastes unter dem Tiefenwinkel
hohen Sendemastes unter dem Tiefenwinkel
 ,
nach ,
nach
 Sekunden unter dem Tiefenwinkel
Sekunden unter dem Tiefenwinkel
 . . |
Der Pilot fliegt mit der gleichbleibenden
Geschwindigkeit von
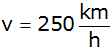 auf horizontalem Kurs parallel zum Erdboden.
auf horizontalem Kurs parallel zum Erdboden. |
|
Fertige eine Skizze an! |
|
|
2 P |
|
|
Aufgabe 5b: |
Der Pilot eines
Sportflugzeuges sieht das Licht an der Spitze eines
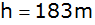 hohen Sendemastes unter dem Tiefenwinkel
hohen Sendemastes unter dem Tiefenwinkel
 ,
nach ,
nach
 Sekunden unter dem Tiefenwinkel
Sekunden unter dem Tiefenwinkel
 . . |
Der Pilot fliegt mit der gleichbleibenden
Geschwindigkeit von
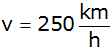 auf horizontalem Kurs parallel zum Erdboden.
auf horizontalem Kurs parallel zum Erdboden. |
In welcher Höhe (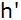 )
flog das Flugzeug? )
flog das Flugzeug? |
|
|
3 P |
|
|
Aufgabe 5c: |
Der Pilot eines
Sportflugzeuges sieht das Licht an der Spitze eines
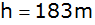 hohen Sendemastes unter dem Tiefenwinkel
hohen Sendemastes unter dem Tiefenwinkel
 ,
nach ,
nach
 Sekunden unter dem Tiefenwinkel
Sekunden unter dem Tiefenwinkel
 . . |
Der Pilot fliegt mit der gleichbleibenden
Geschwindigkeit von
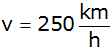 auf horizontalem Kurs parallel zum Erdboden.
auf horizontalem Kurs parallel zum Erdboden. |
Wie weit ( )
war das Flugzeug bei der ersten Peilung von der
Mastspitze entfernt? )
war das Flugzeug bei der ersten Peilung von der
Mastspitze entfernt? |
|
|
3 P |
|
|
Aufgabe 5d: |
Der Pilot eines
Sportflugzeuges sieht das Licht an der Spitze eines
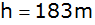 hohen Sendemastes unter dem Tiefenwinkel
hohen Sendemastes unter dem Tiefenwinkel
 ,
nach ,
nach
 Sekunden unter dem Tiefenwinkel
Sekunden unter dem Tiefenwinkel
 . . |
Der Pilot fliegt mit der gleichbleibenden
Geschwindigkeit von
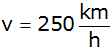 auf horizontalem Kurs parallel zum Erdboden.
auf horizontalem Kurs parallel zum Erdboden. |
Wie lange (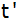 )
dauerte es noch, von der zweiten Peilung an
gemessen, bis sich das Flugzeug senkrecht über der
Mastspitze befand? )
dauerte es noch, von der zweiten Peilung an
gemessen, bis sich das Flugzeug senkrecht über der
Mastspitze befand? |
|
|
3 P |
|
|
Aufgabe 6a: |
| Für einen
Betonpfeiler wird eine Baugrube in Form eines
quadratischen Pyramidenstumpfes ausgeschachtet. |
Es werden
 Erde ausgehoben.
Erde ausgehoben. |
Berechne die obere Breite
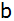 der Grube, wenn sie
der Grube, wenn sie
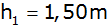 tief ist und die untere Breite
tief ist und die untere Breite
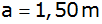 beträgt!
beträgt! |
|
|
4 P |
|
|
Aufgabe 6b: |
| Für einen
Betonpfeiler wird eine Baugrube in Form eines
quadratischen Pyramidenstumpfes ausgeschachtet. |
Es werden
 Erde ausgehoben.
Erde ausgehoben. |
Die Erde wird als kegelförmiger Haufen mit der Höhe
 aufgeschüttet.
aufgeschüttet. |
|
Welche Fläche bedeckt der Erdhaufen? |
|
|
4 P |
|
|
Aufgabe 6c: |
| Für einen
Betonpfeiler wird eine Baugrube in Form eines
quadratischen Pyramidenstumpfes ausgeschachtet. |
Es werden
 Erde ausgehoben.
Erde ausgehoben. |
Die Erde wird als kegelförmiger Haufen mit der Höhe
 aufgeschüttet.
aufgeschüttet. |
Bestimme den Böschungswinkel
 dieses Kegels!
dieses Kegels! |
|
|
3 P |
|
|
Aufgabe 7a: |
Ein senkrechtes
dreiseitiges Prisma, dessen innere Grundfläche ein
gleichseitiges Dreieck mit der Seitenlänge
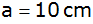 ist, wurde bis zur Höhe
ist, wurde bis zur Höhe
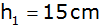 mit Wasser gefüllt.
mit Wasser gefüllt. |
|
In dieses Gefäß wird eine die Wände berührende Kugel
untergetaucht. |
|
Zeichne den Querschnitt durch Prisma und Kugel in
Höhe der Berührpunkte! |
|
|
5 P |
|
|
Aufgabe 7b: |
Ein senkrechtes
dreiseitiges Prisma, dessen innere Grundfläche ein
gleichseitiges Dreieck mit der Seitenlänge
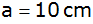 ist, wurde bis zur Höhe
ist, wurde bis zur Höhe
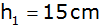 mit Wasser gefüllt.
mit Wasser gefüllt. |
|
In dieses Gefäß wird eine die Wände berührende Kugel
untergetaucht. |
Bis zu welcher Höhe
 steht das Wasser im Prisma nach dem Untertauchen der
Kugel?
steht das Wasser im Prisma nach dem Untertauchen der
Kugel? |
|
|
6 P |
|
|
Aufgabe 8a: |
| Nebenstehende Figur stellt ein
Stehaufmännchen im Achsenschnitt dar. |
Es setzt sich aus einer Halbkugel mit dem
Durchmesser
 , einem Kegelstumpf mit den
Maßen , einem Kegelstumpf mit den
Maßen
 und und
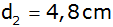 , sowie einem Kugelabschnitt mit
dem Radius , sowie einem Kugelabschnitt mit
dem Radius 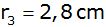 zusammen. zusammen. |
|
Zeichne den Achsenschnitt im Maßstab 1 : 3! |
|
 |
|
|
2 P |
|
|
Aufgabe 8b: |
| Nebenstehende Figur stellt ein
Stehaufmännchen im Achsenschnitt dar. |
Es setzt sich aus einer Halbkugel mit dem
Durchmesser
 ,
einem Kegelstumpf mit den Maßen ,
einem Kegelstumpf mit den Maßen
 und
und
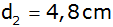 ,
sowie einem Kugelabschnitt mit dem Radius ,
sowie einem Kugelabschnitt mit dem Radius
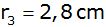 zusammen.
zusammen. |
Berechne die Höhe
 des Kugelabschnitts!
des Kugelabschnitts! |
|
 |
|
|
3 P |
|
|
Aufgabe 8c: |
| Nebenstehende Figur stellt ein
Stehaufmännchen im Achsenschnitt dar. |
Es setzt sich aus einer Halbkugel mit dem
Durchmesser
 ,
einem Kegelstumpf mit den Maßen ,
einem Kegelstumpf mit den Maßen
 und
und
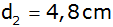 ,
sowie einem Kugelabschnitt mit dem Radius ,
sowie einem Kugelabschnitt mit dem Radius
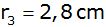 zusammen.
zusammen. |
Welchen Winkel
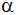 bilden Mantellinie und Grundfläche des
Kegelstumpfes miteinander?
bilden Mantellinie und Grundfläche des
Kegelstumpfes miteinander? |
|
 |
|
|
3 P |
|
|
Aufgabe 8d: |
| Nebenstehende Figur stellt ein
Stehaufmännchen im Achsenschnitt dar. |
Es setzt sich aus einer Halbkugel mit dem
Durchmesser
 ,
einem Kegelstumpf mit den Maßen ,
einem Kegelstumpf mit den Maßen
 und
und
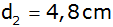 ,
sowie einem Kugelabschnitt mit dem Radius ,
sowie einem Kugelabschnitt mit dem Radius
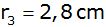 zusammen.
zusammen. |
|
Berechne das Volumen des gesamten Körpers! |
|
 |
|
|
3 P |
|