|
Aufgabe 1a: |
| Das
Anfangsgrundgehalt eines Inspektors in der
Besoldungsgruppe A9 beträgt monatlich 666,32 DM. Es
steigt jeweils nach 2 Jahren um monatlich 29,20 DM.
Dadurch entstehen insgesamt 13 Dienstalterstufen zu
je 2 Jahren mit 24 gleichen Monatsgehältern. |
|
Stelle eine Gehaltstabelle für 26 Dienstjahre mit 13
Stufen auf. |
|
|
1 P |
|
|
Aufgabe 1b: |
| Das
Anfangsgrundgehalt eines Inspektors in der
Besoldungsgruppe A9 beträgt monatlich 666,32 DM. Es
steigt jeweils nach 2 Jahren um monatlich 29,20 DM.
Dadurch entstehen insgesamt 13 Dienstalterstufen zu
je 2 Jahren mit 24 gleichen Monatsgehältern. |
|
Berechne das Monatsgehalt zum Anfang des 25.
Dienstjahres. |
|
|
2 P |
|
|
Aufgabe 1c: |
| Das
Anfangsgrundgehalt eines Inspektors in der
Besoldungsgruppe A9 beträgt monatlich 666,32 DM. Es
steigt jeweils nach 2 Jahren um monatlich 29,20 DM.
Dadurch entstehen insgesamt 13 Dienstalterstufen zu
je 2 Jahren mit 24 gleichen Monatsgehältern. |
|
Welches Gehalt hat der Beamte in den ersten 16
Dienstjahren erhalten? |
|
|
3 P |
|
|
Aufgabe 1d: |
| Das
Anfangsgrundgehalt eines Inspektors in der
Besoldungsgruppe A9 beträgt monatlich 666,32 DM. Es
steigt jeweils nach 2 Jahren um monatlich 29,20 DM.
Dadurch entstehen insgesamt 13 Dienstalterstufen zu
je 2 Jahren mit 24 gleichen Monatsgehältern. |
|
Welches durchschnittliche Monatseinkommen erhält der
Beamte in den ersten 16 Dienstjahren? |
|
|
2 P |
|
|
Aufgabe 1e: |
| Das
Anfangsgrundgehalt eines Inspektors in der
Besoldungsgruppe A9 beträgt monatlich 666,32 DM. Es
steigt jeweils nach 2 Jahren um monatlich 29,20 DM.
Dadurch entstehen insgesamt 13 Dienstalterstufen zu
je 2 Jahren mit 24 gleichen Monatsgehältern. |
|
Wäre der Beamte besser gestellt, wenn seine Bezüge
jedes Jahr um eine halbe Dienstalterszulage, also um
monatlich 14,60 DM, aufgebessert würden? |
|
|
3 P |
|
|
Aufgabe 2a: |
| Ein neuartiger
Ball, der in letzter Zeit auf den Markt kam, springt
jeweils auf 90% seiner vorheriger Fallhöhe zurück.
Man läßt diesen Ball aus 1 m Höhe frei fallen. |
|
Wie oft ist er auf dem Boden aufgesprungen, bis er
zum ersten Male weniger als 20 cm hoch
zurückspringt? |
|
|
5,5 P |
|
|
Aufgabe 2b: |
| Ein neuartiger
Ball, der in letzter Zeit auf den Markt kam, springt
jeweils auf 90% seiner vorheriger Fallhöhe zurück.
Man läßt diesen Ball aus 1 m Höhe frei fallen. |
|
Welchen Gesamtweg legt er bis zu diesem Aufprall
zurück? |
|
|
5,5 P |
|
|
Aufgabe 3a: |
In ein Quadrat
mit der Seitenlänge
 wird ein zweites Quadrat eingezeichnet, indem man
benachbarte Seitenmitten miteinander verbindet.
Fährt man in der gleichen Weise fort, so erhält man
eine Folge von Quadraten.
wird ein zweites Quadrat eingezeichnet, indem man
benachbarte Seitenmitten miteinander verbindet.
Fährt man in der gleichen Weise fort, so erhält man
eine Folge von Quadraten. |
|
Wie groß ist der Umfang des 9. Quadrates dieser
Folge? |
|
|
4 P |
|
|
Aufgabe 3b: |
In ein Quadrat
mit der Seitenlänge
 wird ein zweites Quadrat eingezeichnet, indem man
benachbarte Seitenmitten miteinander verbindet.
Fährt man in der gleichen Weise fort, so erhält man
eine Folge von Quadraten.
wird ein zweites Quadrat eingezeichnet, indem man
benachbarte Seitenmitten miteinander verbindet.
Fährt man in der gleichen Weise fort, so erhält man
eine Folge von Quadraten. |
|
Das wievielte Quadrat der Folge hat einen Umfang von
10 cm? |
|
|
1,5 P |
|
|
Aufgabe 3c: |
In ein Quadrat
mit der Seitenlänge
 wird ein zweites Quadrat eingezeichnet, indem man
benachbarte Seitenmitten miteinander verbindet.
Fährt man in der gleichen Weise fort, so erhält man
eine Folge von Quadraten.
wird ein zweites Quadrat eingezeichnet, indem man
benachbarte Seitenmitten miteinander verbindet.
Fährt man in der gleichen Weise fort, so erhält man
eine Folge von Quadraten. |
|
Wie groß ist die Summe der Umfänge der ersten 8
Quadrate? |
|
|
1,5 P |
|
|
Aufgabe 3d: |
In ein Quadrat
mit der Seitenlänge
 wird ein zweites Quadrat eingezeichnet, indem man
benachbarte Seitenmitten miteinander verbindet.
Fährt man in der gleichen Weise fort, so erhält man
eine Folge von Quadraten.
wird ein zweites Quadrat eingezeichnet, indem man
benachbarte Seitenmitten miteinander verbindet.
Fährt man in der gleichen Weise fort, so erhält man
eine Folge von Quadraten. |
|
Wie groß ist die Summe der Flächen der ersten 8
Quadrate? |
|
|
4 P |
|
|
Aufgabe 4a: |
Auf einer
ebenen Hochfläche steht ein kleiner Sendemast mit
dem Fußpunkt A, abseits in einer Entfernung von 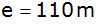 ein größerer Sendemast mit dem Fußpunkt B. Im
Abstand
ein größerer Sendemast mit dem Fußpunkt B. Im
Abstand  von A aus liegt auf der
Verbindungsgeraden beider Fußpunkte eine gemeinsame
Verankerung C für die Halteseile, welche zu den
Mastspitzen führen. von A aus liegt auf der
Verbindungsgeraden beider Fußpunkte eine gemeinsame
Verankerung C für die Halteseile, welche zu den
Mastspitzen führen. |
Das Halteseil für den kleineren Mast bildet den
Höhenwinkel
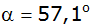 ; das für den größeren den Höhenwinkel ; das für den größeren den Höhenwinkel  (Durchgang bleibt unberücksichtigt).
(Durchgang bleibt unberücksichtigt). |
|
Fertige eine Skizze an. |
|
|
2 P |
|
|
Aufgabe 4b: |
Auf einer
ebenen Hochfläche steht ein kleiner Sendemast mit
dem Fußpunkt A, abseits in einer Entfernung von 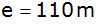 ein größerer Sendemast mit dem Fußpunkt B. Im
Abstand
ein größerer Sendemast mit dem Fußpunkt B. Im
Abstand  von A aus liegt auf der
Verbindungsgeraden beider Fußpunkte eine gemeinsame
Verankerung C für die Halteseile, welche zu den
Mastspitzen führen. von A aus liegt auf der
Verbindungsgeraden beider Fußpunkte eine gemeinsame
Verankerung C für die Halteseile, welche zu den
Mastspitzen führen. |
Das Halteseil für den kleineren Mast bildet den
Höhenwinkel
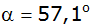 ; das für den größeren den Höhenwinkel ; das für den größeren den Höhenwinkel  (Durchgang bleibt unberücksichtigt).
(Durchgang bleibt unberücksichtigt). |
|
Wie hoch sind die beiden Sendemasten? |
|
|
4 P |
|
|
Aufgabe 4c: |
Auf einer
ebenen Hochfläche steht ein kleiner Sendemast mit
dem Fußpunkt A, abseits in einer Entfernung von 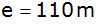 ein größerer Sendemast mit dem Fußpunkt B. Im
Abstand
ein größerer Sendemast mit dem Fußpunkt B. Im
Abstand  von A aus liegt auf der
Verbindungsgeraden beider Fußpunkte eine gemeinsame
Verankerung C für die Halteseile, welche zu den
Mastspitzen führen. von A aus liegt auf der
Verbindungsgeraden beider Fußpunkte eine gemeinsame
Verankerung C für die Halteseile, welche zu den
Mastspitzen führen. |
Das Halteseil für den kleineren Mast bildet den
Höhenwinkel
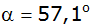 ; das für den größeren den Höhenwinkel ; das für den größeren den Höhenwinkel  (Durchgang bleibt unberücksichtigt).
(Durchgang bleibt unberücksichtigt). |
Unter welchem Steigungswinkel
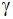 verläuft ein Antennendraht, der von der einen zur
anderen Mastspitze gezogen ist?
verläuft ein Antennendraht, der von der einen zur
anderen Mastspitze gezogen ist? |
|
|
2 P |
|
|
Aufgabe 5a: |
Die beiden
Fahrbahnen der Autobahn sind je
 breit, die Standspur auf jeder Seite
breit, die Standspur auf jeder Seite
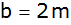 ,
der Mittelstreifen ,
der Mittelstreifen
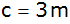 .
Die Autobahn verläuft auf einem Damm von .
Die Autobahn verläuft auf einem Damm von
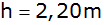 Höhe, der Böschungswinkel beträgt
Höhe, der Böschungswinkel beträgt
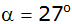 . . |
|
Fertige eine Skizze an. |
|
|
2 P |
|
|
Aufgabe 5b: |
Die beiden
Fahrbahnen der Autobahn sind je
 breit, die Standspur auf jeder Seite
breit, die Standspur auf jeder Seite
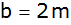 ,
der Mittelstreifen ,
der Mittelstreifen
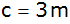 .
Die Autobahn verläuft auf einem Damm von .
Die Autobahn verläuft auf einem Damm von
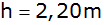 Höhe, der Böschungswinkel beträgt
Höhe, der Böschungswinkel beträgt
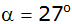 . . |
|
Wie breit wird die Sohle des Damms? |
|
|
3 P |
|
|
Aufgabe 5c: |
Die beiden
Fahrbahnen der Autobahn sind je
 breit, die Standspur auf jeder Seite
breit, die Standspur auf jeder Seite
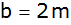 ,
der Mittelstreifen ,
der Mittelstreifen
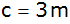 .
Die Autobahn verläuft auf einem Damm von .
Die Autobahn verläuft auf einem Damm von
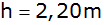 Höhe, der Böschungswinkel beträgt
Höhe, der Böschungswinkel beträgt
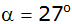 . . |
Wie groß ist die Böschungslänge
 ? ? |
|
|
2 P |
|
|
Aufgabe 5d: |
Die beiden
Fahrbahnen der Autobahn sind je
 breit, die Standspur auf jeder Seite
breit, die Standspur auf jeder Seite
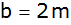 ,
der Mittelstreifen ,
der Mittelstreifen
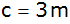 .
Die Autobahn verläuft auf einem Damm von .
Die Autobahn verläuft auf einem Damm von
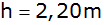 Höhe, der Böschungswinkel beträgt
Höhe, der Böschungswinkel beträgt
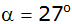 . . |
Wieviel Fuhren Erde zu je
 sind für
sind für
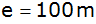 Damm erforderlich?
Damm erforderlich? |
|
|
4 P |
|
|
Aufgabe 6a: |
Ein Kübel hat
unten eine lichte Weite von
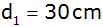 ,
oben eine von ,
oben eine von
 .
Seine Seitenlinie ist .
Seine Seitenlinie ist
 lang.
lang. |
|
Zeichne einen Achsenschnitt des Körpers im Maßstab 1
: 10. |
|
|
3 P |
|
|
Aufgabe 6b: |
Ein Kübel hat
unten eine lichte Weite von
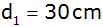 ,
oben eine von ,
oben eine von
 .
Seine Seitenlinie ist .
Seine Seitenlinie ist
 lang.
lang. |
|
Wieviel Liter faßt der Kübel, wenn er bis zur halben
Höhe gefüllt ist? |
|
|
4P |
|
|
Aufgabe 6c: |
Ein Kübel hat
unten eine lichte Weite von
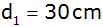 ,
oben eine von ,
oben eine von
 .
Seine Seitenlinie ist .
Seine Seitenlinie ist
 lang.
lang. |
|
Wieviel Prozent des Gesamtvolumens sind mit Wasser
gefüllt? |
|
|
4 P |
|
|
Aufgabe 7a: |
In einem
halbkugelförmigen Becken mit dem Radius
 liegt eine Eisenkugel mit dem Radius
liegt eine Eisenkugel mit dem Radius
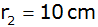 . . |
|
Zeichne einen Achsenschnitt im Maßstab 1 : 10. |
|
|
4 P |
|
|
Aufgabe 7b: |
In einem
halbkugelförmigen Becken mit dem Radius
 liegt eine Eisenkugel mit dem Radius
liegt eine Eisenkugel mit dem Radius
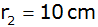 . . |
|
Wieviel Liter Wasser muß man in das Becken gießen,
damit die Kugel gerade bedeckt wird? |
|
|
7 P |
|
|
Aufgabe 8a: |
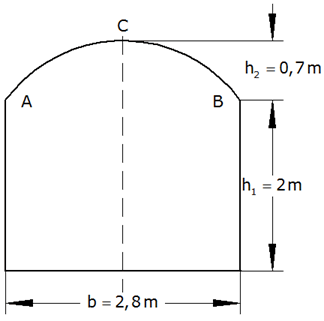
| Untenstehende Skizze stellt
den Querschnitt durch einen Keller dar. |
|
 |
|
Berechne den Gewölberadius r. |
|
|
|
|
Aufgabe 8b: |
| Untenstehende Skizze stellt
den Querschnitt durch einen Keller dar. |
|
 |
|
Fertige eine eigene Zeichnung im Maßstab 1 : 100 an und
trage den Radius zu den Peripheriepunkten A, B und C ein. |
|
|
|
|
Aufgabe 8c: |
| Untenstehende Skizze stellt
den Querschnitt durch einen Keller dar. |
|
 |
Welches Fassungsvermögen hat der Keller, wenn er
 lang
ist? lang
ist? |
|
|
|