|
|
|
Aufgabe 2: |
| Eine kleine
Talsperre kann dadurch gefüllt werden, daß der eine
Zufluß 16 Tage, der andere aber nur 10 Tage geöffnet
ist. Die Füllung kann auch so geschehen, daß der
zweite Zufluß 25 Tage, der erste jedoch nur 4 Tage
Wasser zuführt. |
|
In wieviel Tagen füllt jeder Zufluß für sich die
Talsperre? |
|
|
2 P |
|
|
Aufgabe 3: |
| Um ein 100 m
langes und 20 m breites Schwimmbecken führt für die
Zuschauer ringsherum ein Streifen, der an der
Schmalseite 1,5mal so breit wie an der Längsseite
ist. |
Wie sind die Maße des Streifens zu wählen, wenn für
die Gesamtanlage ein Gelände von
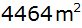 zur Verfügung steht?
zur Verfügung steht? |
|
|
2 P |
|
|
Aufgabe 4: |
| Ein
Textilkaufmann kauft für 2000 DM Ware, die er mit x
Prozent Gewinn verkauft. Für den Erlös kauft er
weitere Ware und setzt sie mit demselben
Gewinnprozentsatz wieder ab. |
|
Wieviel Prozent betrug der Gewinn, wenn der Kaufmann
nach dem Verkauf der Ware 2880 DM hatte? |
|
|
2 P |
|
|
Aufgabe 5a: |
| Ein Sportverein
mietete für einen Ausflug einen Omnibus für 380 DM. |
|
Da zwei Mitglieder wegen plötzlicher Erkrankung
nicht teilnehmen konnten, erhöhte sich der
ursprüngliche Fahrpreis für jeden Teilnehmer um 0,50
DM. |
|
Wieviel Personen nahmen am Ausflug teil? |
|
|
2 P |
|
|
Aufgabe 5b: |
| Ein Sportverein
mietete für einen Ausflug einen Omnibus für 380 DM. |
|
Da zwei Mitglieder wegen plötzlicher Erkrankung
nicht teilnehmen konnten, erhöhte sich der
ursprüngliche Fahrpreis für jeden Teilnehmer um 0,50
DM. |
|
Wie hoch war der anteilige Fahrpreis? |
|
|
2 P |
|
|
Aufgabe 6a: |
| 850 g 8%-iger
Sole soll mit 750 g 11%-iger und 780 g 12%-iger Sole
gemischt werden. |
|
Welcher Salzgehalt in Prozent hat die Mischung? |
|
|
2 P |
|
|
Aufgabe 6b: |
| 850 g 8%-iger
Sole soll mit 750 g 11%-iger und 780 g 12%-iger Sole
gemischt werden. |
|
Wieviel Wasser ist der Mischung zuzufügen, um eine
10%-ige Sole zu erhalten? |
|
|
2 P |
|
|
Aufgabe 7: |
Von einem
Steilhang stürzt ein Felsblock in einen 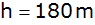 tiefen
Abgrund. tiefen
Abgrund. |
Nach welcher Zeit t hört man an der Abbruchstelle
den Felsblock unten aufschlagen
(Schallgeschwindigkeit
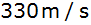 , ,
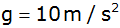 )? )? |
|
|
2 P |
|
|
Aufgabe 8a: |
| Ein Vermögen
von 4950 DM soll unter 6 Personen so verteilt
werden, daß jede folgende Person eine bestimmte
Summe weniger als die vorhergehende erhält. |
|
Die erste Person bekommt 1200 DM. |
|
Wieviel DM erhält die letzte Person? |
|
|
2 P |
|
|
Aufgabe 8b: |
| Ein Vermögen
von 4950 DM soll unter 6 Personen so verteilt
werden, daß jede folgende Person eine bestimmte
Summe weniger als die vorhergehende erhält. |
|
Die erste Person bekommt 1200 DM. |
|
Wie groß ist der Unterschied der Teilbeträge? |
|
|
2 P |
|
|
Aufgabe 9a: |
| Unter 7
Personen sollen 14000 DM so verteilt werden, daß
jede folgende Person um den gleichen Betrag weniger
bekommt als die vorhergehende. |
|
Die erste Person erhält 3500 DM. |
|
Wie groß ist der letzte Teilbetrag? |
|
|
2 P |
|
|
Aufgabe 9b: |
| Unter 7
Personen sollen 14000 DM so verteilt werden, daß
jede folgende Person um den gleichen Betrag weniger
bekommt als die vorhergehende. |
|
Die erste Person erhält 3500 DM. |
|
Wieviel bekommen die anderen Personen? |
|
|
2 P |
|
|
Aufgabe 10a: |
| Papier von der
Stärke 0,1 mm ist auf eine Rolle gewickelt worden,
die einen Durchmesser von 12 cm hat. Einschließlich
des Papiers ist die Rolle 25 cm dick. |
|
Wieviel Lagen bildet das Papier auf der Rolle? |
|
|
2 P |
|
|
Aufgabe 10b: |
| Papier von der
Stärke 0,1 mm ist auf eine Rolle gewickelt worden,
die einen Durchmesser von 12 cm hat. Einschließlich
des Papiers ist die Rolle 25 cm dick. |
|
Berechne die Gesamtlänge des aufgewickelten Papiers. |
|
|
2 P |
|
|
Aufgabe 11a: |
| Aus einem
Gefäß, das 75 Liter reinen Alkohol enthält, werden 5
Liter entnommen und durch die gleiche Menge Wasser
ersetzt. Das Verfahren wird in derselben Weise
mehrfach wiederholt. |
|
Wieviel Liter Alkohol befinden sich nach der 10ten
Verdünnung noch im Gefäß? |
|
|
2 P |
|
|
Aufgabe 11b: |
| Aus einem
Gefäß, das 75 Liter reinen Alkohol enthält, werden 5
Liter entnommen und durch die gleiche Menge Wasser
ersetzt. Das Verfahren wird in derselben Weise
mehrfach wiederholt. |
|
Wie hoch ist dann der Alkoholgehalt der Mischung in
Prozent (des Gesamtvolumens)? |
|
|
2 P |
|
|
Aufgabe 12a: |
| Ein Gefäß
enthält 200 Liter reinen Alkohol. Man füllt 25 Liter
ab und ersetzt sie durch Wasser. Von der Mischung
werden wieder 25 Liter entnommen und durch Wasser
ersetzt. Das Verfahren wird im ganzen 10mal
durchgeführt. |
|
Wieviel Liter Alkohol befinden sich anschließend noch im Gefäß? |
|
|
2 P |
|
|
Aufgabe 12b: |
| Ein Gefäß
enthält 200 Liter reinen Alkohol. Man füllt 25 Liter
ab und ersetzt sie durch Wasser. Von der Mischung
werden wieder 25 Liter entnommen und durch Wasser
ersetzt. Das Verfahren wird im ganzen 10mal
durchgeführt. |
|
Wieviel Prozent des Gesamtvolumens der Mischung sind
Alkohol? |
|
|
2 P |
|
|
Aufgabe 13a: |
| Ein Lichtstrahl
durchdringt gleichstarke aufeinanderliegende
Glasplatten. Beim Durchdringen je einer Glasplatte
verliert dieser Lichtstrahl 10 Prozent seiner
vorherigen Helligkeit. |
|
Wieviel Prozent seiner ursprünglichen Helligkeit
besitzt er noch nach dem Durchgang durch 10 Platten? |
|
|
2 P |
|
|
Aufgabe 13b: |
| Ein Lichtstrahl
durchdringt gleichstarke aufeinanderliegende
Glasplatten. Beim Durchdringen je einer Glasplatte
verliert dieser Lichtstrahl 10 Prozent seiner
vorherigen Helligkeit. |
|
Nach wieviel Platten ist seine Helligkeit auf 20
Prozent seiner ursprünglichen Helligkeit abgesunken? |
|
|
2 P |
|
|
Aufgabe 14: |
| Kaufmann Maier
legte am 1.1.1964 für das Studium seiner 3 Söhne
35000 DM zu 3,5% auf Zinseszins an. 3 Jahre lang
werden am Ende jeden Jahres 5500 DM abgehoben. Am
Ende des 4. Jahres wird der Vermögensrest unter die
3 Söhne aufgeteilt. |
|
Welchen Betrag B erhält jeder von diesem Rest? |
|
|
2 P |
|
|
Aufgabe 15a: |
| Einem
Sparbetrag von 2500 DM werden nach 1 Jahr die Zinsen
gutgeschrieben, dann liegt er ein weiteres Jahr auf
der Sparkasse. Am Ende des zweiten Jahres können
insgesamt 2704 DM abgehoben werden. |
|
Berechne den Zinsfuß. |
|
|
2 P |
|
|
Aufgabe 15b: |
| Einem
Sparbetrag von 2500 DM werden nach 1 Jahr die Zinsen
gutgeschrieben, dann liegt er ein weiteres Jahr auf
der Sparkasse. Am Ende des zweiten Jahres können
insgesamt 2704 DM abgehoben werden. |
|
Welcher Betrag hätte 9 Monate später abgehoben
werden können? |
|
|
2 P |
|
|
Aufgabe 16: |
| Ein Handwerker
hat zur Neueinrichtung einer Werkstatt ein 5%-iges
Darlehen von 3000 DM bei einer Sparkasse
aufgenommen. Es soll in 6 gleichen jährlichen
Tilgungsraten, die vom Ende des 2. Jahres ab nach
Gewährung des Darlehens zahlbar sind, zurückgezahlt
werden. |
|
Wie hoch sind die Tilgungsraten? |
|
|
2 P |
|
|
Aufgabe 17a: |
Herr Kluge
zahlt am Ende eines jeden Jahres einen bestimmten
Betrag r auf sein Bankkonto ein. Am Ende des 5.
Jahres kauft er einen Lastkraftwagen und überweist
den Kaufpreis von
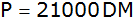 ;
auf seinem Konto bleiben noch ;
auf seinem Konto bleiben noch
 übrig.
übrig. |
|
Welcher Betrag wurde am Ende eines jeden Jahres
eingezahlt, wenn 4% Zinseszinsen berechnet wurden? |
|
|
2 P |
|
|
Aufgabe 17b: |
Herr Kluge
zahlt am Ende eines jeden Jahres einen bestimmten
Betrag r auf sein Bankkonto ein. Am Ende des 5.
Jahres kauft er einen Lastkraftwagen und überweist
den Kaufpreis von
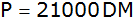 ;
auf seinem Konto bleiben noch ;
auf seinem Konto bleiben noch
 übrig.
übrig. |
|
Nach weiteren 5 Jahren wird der Lastkraftwagen für
11000 DM verkauft. Wieviel Prozent Wertminderung
(Abschreibung) wurden jährlich berechnet? |
|
|
2 P |
|
|
Aufgabe 18: |
| Herr A kauft
ein Haus. Er hat dafür entweder 3 Raten zu je 40000
DM zu zahlen, und zwar die 1. Rate sofort, die 2.
Rate nach 2 Jahren und die 3. Rate nach 4 Jahren;
oder er hat nach 3 Jahren eine einmalige Zahlung in
Höhe von 126500 DM zu leisten. |
|
Welche Zahlungsart wird er bevorzugen, wenn er das
Geld zu 5,5% angelegt hat? |
|
|
2 P |
|
|
Aufgabe 19a: |
Gegeben ist
eine Gerade durch  und und
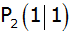 . . |
|
Gesucht ist der Geradenpunkt, der auf der y-Achse
liegt. |
|
|
2 P |
|
|
Aufgabe 19b: |
Gegeben ist
eine Gerade durch  und und
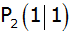 . . |
|
Gesucht ist der Geradenpunkt, der auf der x-Achse
liegt. |
|
|
2 P |
|
|
Aufgabe 19c: |
Gegeben ist
eine Gerade durch  und und
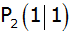 . . |
Bestimme die Länge
 des Ausschnittes, den die Koordinatenachsen auf der
Geraden erzeugen.
des Ausschnittes, den die Koordinatenachsen auf der
Geraden erzeugen. |
|
|
2 P |
|
|
Aufgabe 20a: |
Konstruiere das
gleichschenkligrechtwinklige Dreieck ABC mit der
Hypotenuse
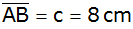 . . |
Beschreibe um C den Kreisbogen, der
 als Sehne besitzt. Schlage ferner über den Katheten
a des Dreiecks die Halbkreise, die außerhalb des
Dreiecks liegen.
als Sehne besitzt. Schlage ferner über den Katheten
a des Dreiecks die Halbkreise, die außerhalb des
Dreiecks liegen. |
|
|
2 P |
|
|
Aufgabe 20b: |
Konstruiere das
gleichschenkligrechtwinklige Dreieck ABC mit der
Hypotenuse
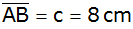 . . |
Beschreibe um C den Kreisbogen, der
 als Sehne besitzt. Schlage ferner über den Katheten
a des Dreiecks die Halbkreise, die außerhalb des
Dreiecks liegen.
als Sehne besitzt. Schlage ferner über den Katheten
a des Dreiecks die Halbkreise, die außerhalb des
Dreiecks liegen. |
|
Berechne den Inhalt F der von den gezeichneten
Kreisbögen umschlossenen Fläche. |
|
|
2 P |
|
|
Aufgabe 21: |
Berechne die
Masse m eines Rundeisenstückes, dessen Oberfläche O
mit
 und dessen Mantel M mit
und dessen Mantel M mit
 gegeben sind (
gegeben sind (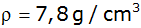 ). ). |
|
|
2 P |
|
|
Aufgabe 22a: |
Das Mauerwerk
eines
 langen Tunnels ist
langen Tunnels ist
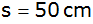 dick und hat die Form eines halben Hohlzylinders.
Der große Durchmesser D beträgt 6 m.
dick und hat die Form eines halben Hohlzylinders.
Der große Durchmesser D beträgt 6 m. |
Wieviel
 Mauerwerk sind für den Bau erforderlich?
Mauerwerk sind für den Bau erforderlich? |
|
|
2 P |
|
|
Aufgabe 22b: |
Das Mauerwerk
eines
 langen Tunnels ist
langen Tunnels ist
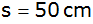 dick und hat die Form eines halben Hohlzylinders.
Der große Durchmesser D beträgt 6 m.
dick und hat die Form eines halben Hohlzylinders.
Der große Durchmesser D beträgt 6 m. |
Wieviel Steine
benötigt man, wenn auf 1
 Mauerwerk rund 385 Stück gerechnet werden?
Mauerwerk rund 385 Stück gerechnet werden? |
|
|
2 P |
|
|
Aufgabe 22c: |
Das Mauerwerk
eines
 langen Tunnels ist
langen Tunnels ist
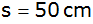 dick und hat die Form eines halben Hohlzylinders.
Der große Durchmesser D beträgt 6 m.
dick und hat die Form eines halben Hohlzylinders.
Der große Durchmesser D beträgt 6 m. |
Wieviel
 Luft faßt der eingeschlossene Raum?
Luft faßt der eingeschlossene Raum? |
|
|
2 P |
|
|
Aufgabe 23: |
|
Das Dach eines Gartenhäuschens hat die Gestalt einer
regelmäßigen sechsseitigen Pyramide. Die Traufenkante mißt
1,50 m, die Höhe h 0,80 m. |
|
Wieviel Teerpappe werden zum Abdecken des Daches
insgesamt benötigt, wenn man für Verschnitt 12,5% der
Fertigmaße ansetzt? |
|
2 P |
|
|
Aufgabe 24: |
Ein Bergkristall (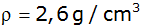 )
setzt sich zusammen aus einem regelmäßigen sechseckigen
Prisma (Höhe )
setzt sich zusammen aus einem regelmäßigen sechseckigen
Prisma (Höhe
 ) und
beiderseits aufgesetzten sechseckigen Pyramiden (Höhe ) und
beiderseits aufgesetzten sechseckigen Pyramiden (Höhe
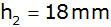 ). ).
Der Kristall wiegt 17,3 g. |
|
Wie lang ist seine Grundkante a? |
|
2 P |
|
|
Aufgabe 25: |
Ein Bleistück (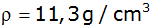 )
von der Form eines quadratischen Pyramidenstumpfes mit der
Höhe )
von der Form eines quadratischen Pyramidenstumpfes mit der
Höhe
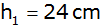 und den Kanten
und den Kanten
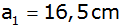 , ,
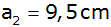 soll
in einen Hohlzylinder mit soll
in einen Hohlzylinder mit
 , ,
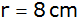 umgegossen werden.
umgegossen werden. |
|
Berechne die Höhe h des Hohlzylinders und seine Masse m. |
|
2 P |
|
|
Aufgabe 26a: |
|
Ein geschlossenes Werkstück (Kegelstumpf mit aufgesetztem
Kegel) soll aus Kupferblech hergestellt werden. |
Die Maße sind: Durchmesser
 der
Grundfläche des Kegelstumpfes 66 cm, Durchmesser der
Grundfläche des Kegelstumpfes 66 cm, Durchmesser
 der
Grundfläche des Kegels 48 cm, die Höhe H des ganzen
Werkstücks 22 cm, die Höhe der
Grundfläche des Kegels 48 cm, die Höhe H des ganzen
Werkstücks 22 cm, die Höhe
 des
Kegels des
Kegels
 der
Höhe der
Höhe
 des Kegelstumpfes.
des Kegelstumpfes. |
|
Zeichne einen Achsenschnitt des Werkstücks im Maßstab 1 :
10. |
|
2 P |
|
|
Aufgabe 26b: |
|
Ein geschlossenes Werkstück (Kegelstumpf mit aufgesetztem
Kegel) soll aus Kupferblech hergestellt werden. |
Die Maße sind: Durchmesser
 der
Grundfläche des Kegelstumpfes 66 cm, Durchmesser der
Grundfläche des Kegelstumpfes 66 cm, Durchmesser
 der
Grundfläche des Kegels 48 cm, die Höhe H des ganzen
Werkstücks 22 cm, die Höhe der
Grundfläche des Kegels 48 cm, die Höhe H des ganzen
Werkstücks 22 cm, die Höhe
 des
Kegels des
Kegels
 der
Höhe der
Höhe
 des Kegelstumpfes.
des Kegelstumpfes. |
Berechne die Mantellinien des Kegelstumpfes
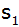 und des Kegels
und des Kegels
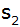 . . |
|
2 P |
|
|
Aufgabe 26c: |
|
Ein geschlossenes Werkstück (Kegelstumpf mit aufgesetztem
Kegel) soll aus Kupferblech hergestellt werden. |
Die Maße sind: Durchmesser
 der
Grundfläche des Kegelstumpfes 66 cm, Durchmesser der
Grundfläche des Kegelstumpfes 66 cm, Durchmesser
 der
Grundfläche des Kegels 48 cm, die Höhe H des ganzen
Werkstücks 22 cm, die Höhe der
Grundfläche des Kegels 48 cm, die Höhe H des ganzen
Werkstücks 22 cm, die Höhe
 des
Kegels des
Kegels
 der
Höhe der
Höhe
 des Kegelstumpfes.
des Kegelstumpfes. |
Wieviel
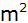 Kupferblech werden zur nahtlosen Herstellung benötigt?
Kupferblech werden zur nahtlosen Herstellung benötigt? |
|
2 P |
|
|
Aufgabe 26d: |
|
Ein geschlossenes Werkstück (Kegelstumpf mit aufgesetztem
Kegel) soll aus Kupferblech hergestellt werden. |
Die Maße sind: Durchmesser
 der
Grundfläche des Kegelstumpfes 66 cm, Durchmesser der
Grundfläche des Kegelstumpfes 66 cm, Durchmesser
 der
Grundfläche des Kegels 48 cm, die Höhe H des ganzen
Werkstücks 22 cm, die Höhe der
Grundfläche des Kegels 48 cm, die Höhe H des ganzen
Werkstücks 22 cm, die Höhe
 des
Kegels des
Kegels
 der
Höhe der
Höhe
 des Kegelstumpfes.
des Kegelstumpfes. |
Welche Masse haben 50 Werkstücke, wenn
 Kupferblech 8,9 kg an Masse hat?
Kupferblech 8,9 kg an Masse hat? |
|
2 P |
|
|
Aufgabe 27a: |
Eine Kugel, deren Rauminhalt
 beträgt, wird von einer Ebene geschnitten, die vom
Mittelpunkt der Kugel einen Abstand von a = 8 cm besitzt.
beträgt, wird von einer Ebene geschnitten, die vom
Mittelpunkt der Kugel einen Abstand von a = 8 cm besitzt. |
|
Berechne den Radius r der Kugel. |
|
2 P |
|
|
Aufgabe 27b: |
Eine Kugel, deren Rauminhalt
 beträgt, wird von einer Ebene geschnitten, die vom
Mittelpunkt der Kugel einen Abstand von a = 8 cm besitzt.
beträgt, wird von einer Ebene geschnitten, die vom
Mittelpunkt der Kugel einen Abstand von a = 8 cm besitzt. |
Wie groß ist der Radius
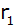 der Schnittfläche?
der Schnittfläche? |
|
2 P |
|
|
Aufgabe 27c: |
Eine Kugel, deren Rauminhalt
 beträgt, wird von einer Ebene geschnitten, die vom
Mittelpunkt der Kugel einen Abstand von a = 8 cm besitzt.
beträgt, wird von einer Ebene geschnitten, die vom
Mittelpunkt der Kugel einen Abstand von a = 8 cm besitzt. |
|
Wie groß ist der Inhalt F der Schnittfläche? |
|
2 P |
|
|
Aufgabe 27d: |
Eine Kugel, deren Rauminhalt
 beträgt, wird von einer Ebene geschnitten, die vom
Mittelpunkt der Kugel einen Abstand von a = 8 cm besitzt.
beträgt, wird von einer Ebene geschnitten, die vom
Mittelpunkt der Kugel einen Abstand von a = 8 cm besitzt. |
|
Welche Bahngeschwindigkeit v hat ein Punkt des Kreisumfangs
der Schnittfläche, wenn sich die Kugel in einer Minute 20mal
um die Achse dreht, die senkrecht zur Schnittfläche steht? |
|
2 P |
|
|
Aufgabe 28: |
Auf einem quadratischen Pyramidenstumpf mit der unteren
Kante von
 , der
oberen von , der
oberen von
 und
dem Neigungswinkel und
dem Neigungswinkel
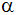 seiner Seitenfläche gegen die Grundfläche von
seiner Seitenfläche gegen die Grundfläche von
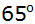 steht ein Kegelstumpf von
steht ein Kegelstumpf von
 Höhe. Sein Grundkreisradius ist
Höhe. Sein Grundkreisradius ist
 , der
Neigungswinkel , der
Neigungswinkel
 seiner Mantellinie gegen die Grundfläche beträgt
seiner Mantellinie gegen die Grundfläche beträgt
 . . |
Welche Masse m hat der gesamte Körper aus Stahl ( )? )? |
|
2 P |
|
|
Aufgabe 29a: |
Ein rechtwinkliges Dreieck mit den Katheten
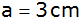 , ,
 wird um die Kathete a gedreht.
wird um die Kathete a gedreht. |
|
Zeichne einen Achsenschnitt des Drehkörpers (Einheit = 1
cm). |
|
2 P |
|
|
Aufgabe 29b: |
Ein rechtwinkliges Dreieck mit den Katheten
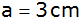 , ,
 wird um die Kathete a gedreht.
wird um die Kathete a gedreht. |
|
Berechne die Oberfläche O und das Volumen V des Körpers. |
|
2 P |
|
|
Aufgabe 29c: |
Ein rechtwinkliges Dreieck mit den Katheten
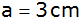 , ,
 wird um die Kathete a gedreht.
wird um die Kathete a gedreht. |
Wie groß ist der Neigungswinkel
 der
Seitenlinie gegen die Grundfläche? der
Seitenlinie gegen die Grundfläche? |
|
2 P |
|
|
Aufgabe 29d: |
Ein rechtwinkliges Dreieck mit den Katheten
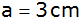 , ,
 wird um die Kathete a gedreht.
wird um die Kathete a gedreht. |
|
Welcher Körper entsteht, wenn das Dreieck um die Hypotenuse
gedreht wird? |
|
2 P |
|
|
Aufgabe 30a: |
Von einem
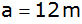 hohen Balkon eines Hauses aus wird der Fußpunkt eines Turmes
unter einem Tiefenwinkel von
hohen Balkon eines Hauses aus wird der Fußpunkt eines Turmes
unter einem Tiefenwinkel von
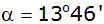 ,
die Spitze unter einem Erhebungswinkel von ,
die Spitze unter einem Erhebungswinkel von
 anvisiert.
anvisiert. |
|
Haus und Turm stehen auf derselben Horizontalebene. |
|
Wie weit (e) ist der Turm vom Haus entfernt? |
|
2 P |
|
|
Aufgabe 30b: |
Von einem
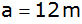 hohen Balkon eines Hauses aus wird der Fußpunkt eines Turmes
unter einem Tiefenwinkel von
hohen Balkon eines Hauses aus wird der Fußpunkt eines Turmes
unter einem Tiefenwinkel von
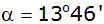 ,
die Spitze unter einem Erhebungswinkel von ,
die Spitze unter einem Erhebungswinkel von
 anvisiert.
anvisiert.
Haus und Turm stehen auf derselben
Horizontalebene. |
|
Wie hoch (h) ist der Turm? |
|
2 P |
|
|
Aufgabe 31a: |
Vom Rande einer Plattform eines
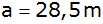 hohen Turmes aus erscheint der Fußpunkt einer senkrechten
Felswand unter einem Tiefenwinkel von
hohen Turmes aus erscheint der Fußpunkt einer senkrechten
Felswand unter einem Tiefenwinkel von
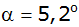 ,
ihr höchster Punkt unter einem Erhebungswinkel von ,
ihr höchster Punkt unter einem Erhebungswinkel von
 . . |
|
Turm und Felswand stehen auf derselben Horizontalebene. |
|
Wie weit (e) ist die Felswand von dem Turm entfernt? |
|
2 P |
|
|
Aufgabe 31b: |
Vom Rande einer Plattform eines
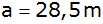 hohen Turmes aus erscheint der Fußpunkt einer senkrechten
Felswand unter einem Tiefenwinkel von
hohen Turmes aus erscheint der Fußpunkt einer senkrechten
Felswand unter einem Tiefenwinkel von
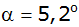 ,
ihr höchster Punkt unter einem Erhebungswinkel von ,
ihr höchster Punkt unter einem Erhebungswinkel von
 . . |
|
Turm und Felswand stehen auf derselben Horizontalebene. |
|
Wie hoch (h) ist die Felswand? |
|
2 P |
|
|
Aufgabe 32a: |
Ein Sendemast wird durch
 lange Seile am Boden verankert. Diese Seile sind
lange Seile am Boden verankert. Diese Seile sind
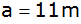 unterhalb der Spitze befestigt und bilden einen Winkel von
unterhalb der Spitze befestigt und bilden einen Winkel von
 mit
der Waagerechten. mit
der Waagerechten. |
|
Wie hoch (h) ist der Mast? |
|
2 P |
|
|
Aufgabe 32b: |
Ein Sendemast wird durch
 lange Seile am Boden verankert. Diese Seile sind
lange Seile am Boden verankert. Diese Seile sind
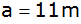 unterhalb der Spitze befestigt und bilden einen Winkel von
unterhalb der Spitze befestigt und bilden einen Winkel von
 mit
der Waagerechten. mit
der Waagerechten. |
|
In welcher Entfernung (e) vom Fuß des Mastes sind die Seile
im Boden verankert? |
|
2 P |
|
|
Aufgabe 32c: |
Ein Sendemast wird durch
 lange Seile am Boden verankert. Diese Seile sind
lange Seile am Boden verankert. Diese Seile sind
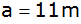 unterhalb der Spitze befestigt und bilden einen Winkel von
unterhalb der Spitze befestigt und bilden einen Winkel von
 mit
der Waagerechten. mit
der Waagerechten. |
Bei welcher Sonnenhöhe (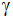 )
ist der Schatten des Mastes )
ist der Schatten des Mastes
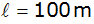 lang?
lang? |
|
2 P |
|
|
Aufgabe 33a: |
Die Einfahrt zu einer Kellergarage, deren Boden
 unter der Straßenoberfläche liegt, hat ein Gefälle von 20%.
unter der Straßenoberfläche liegt, hat ein Gefälle von 20%. |
Wie weit (e) ist die Garageneinfahrt von der Straße entfernt
und wie groß ist der Steigungswinkel
 ? ? |
|
2 P |
|
|
Aufgabe 33b: |
Die Einfahrt zu einer Kellergarage, deren Boden
 unter der Straßenoberfläche liegt, hat ein Gefälle von 20%.
unter der Straßenoberfläche liegt, hat ein Gefälle von 20%. |
|
Wie lang ist die Auffahrt von der Garage zur Straße? |
|
2 P |
|
|
Aufgabe 34a: |
Ein
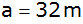 hoher Turm steht
hoher Turm steht
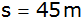 von
einem Fluss entfernt. Von der Turmspitze aus erscheint die
Flußbreite unter einem Sehwinkel von von
einem Fluss entfernt. Von der Turmspitze aus erscheint die
Flußbreite unter einem Sehwinkel von
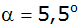 .
Unmittelbar am jenseitigen Ufer erblickt man eine Pappel,
deren Wipfel unter einem Tiefenwinkel von .
Unmittelbar am jenseitigen Ufer erblickt man eine Pappel,
deren Wipfel unter einem Tiefenwinkel von
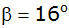 von
der Turmspitze aus zu sehen ist. von
der Turmspitze aus zu sehen ist. |
|
Wie breit (b) ist der Fluß? |
|
2 P |
|
|
Aufgabe 34b: |
Ein
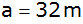 hoher Turm steht
hoher Turm steht
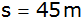 von
einem Fluss entfernt. Von der Turmspitze aus erscheint die
Flußbreite unter einem Sehwinkel von von
einem Fluss entfernt. Von der Turmspitze aus erscheint die
Flußbreite unter einem Sehwinkel von
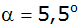 .
Unmittelbar am jenseitigen Ufer erblickt man eine Pappel,
deren Wipfel unter einem Tiefenwinkel von .
Unmittelbar am jenseitigen Ufer erblickt man eine Pappel,
deren Wipfel unter einem Tiefenwinkel von
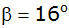 von
der Turmspitze aus zu sehen ist. von
der Turmspitze aus zu sehen ist. |
|
Wie hoch (h) ist die Pappel? |
|
2 P |
|
|
Aufgabe 35a: |
An der Küste eines Hafenortes ist eine horizontale
Standlinie
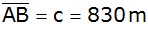 abgesteckt. Von ihren Endpunkten aus wird ein
vorüberfahrendes Schiff (S) zum gleichen Zeitpunkt
angepeilt. Die Peilrichtungen bilden mit der Standlinie die
Winkel
abgesteckt. Von ihren Endpunkten aus wird ein
vorüberfahrendes Schiff (S) zum gleichen Zeitpunkt
angepeilt. Die Peilrichtungen bilden mit der Standlinie die
Winkel
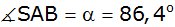 und und
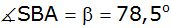 . . |
|
In welcher Entfernung (b) von A befindet sich das Schiff zum
Zeitpunkt der Beobachtung? |
|
2 P |
|
|
Aufgabe 35b: |
An der Küste eines Hafenortes ist eine horizontale
Standlinie
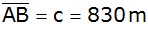 abgesteckt. Von ihren Endpunkten aus wird ein
vorüberfahrendes Schiff (S) zum gleichen Zeitpunkt
angepeilt. Die Peilrichtungen bilden mit der Standlinie die
Winkel
abgesteckt. Von ihren Endpunkten aus wird ein
vorüberfahrendes Schiff (S) zum gleichen Zeitpunkt
angepeilt. Die Peilrichtungen bilden mit der Standlinie die
Winkel
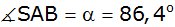 und und
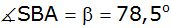 . . |
|
In welcher Entfernung (a) von B befindet sich das Schiff zum
Zeitpunkt der Beobachtung? |
|
2 P |
|
|
Aufgabe 35c: |
An der Küste eines Hafenortes ist eine horizontale
Standlinie
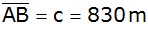 abgesteckt. Von ihren Endpunkten aus wird ein
vorüberfahrendes Schiff (S) zum gleichen Zeitpunkt
angepeilt. Die Peilrichtungen bilden mit der Standlinie die
Winkel
abgesteckt. Von ihren Endpunkten aus wird ein
vorüberfahrendes Schiff (S) zum gleichen Zeitpunkt
angepeilt. Die Peilrichtungen bilden mit der Standlinie die
Winkel
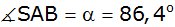 und und
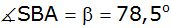 . . |
|
In welchem Abstand (h) von der Standlinie befindet sich das
Schiff zum Zeitpunkt der Beobachtung? |
|
2 P |
|
|
Aufgabe 36a: |
Ein Siedlungsgelände hat die Form eines Dreiecks. Seine
Seiten sind
 , ,
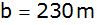 , ,
 lang. Von der Mitte der längsten Seite aus wird ein Weg zur
gegenüberliegenden Ecke angelegt.
lang. Von der Mitte der längsten Seite aus wird ein Weg zur
gegenüberliegenden Ecke angelegt. |
Berechne die Länge (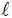 )
des Weges. )
des Weges. |
|
2 P |
|
|
Aufgabe 36b: |
Ein Siedlungsgelände hat die Form eines Dreiecks. Seine
Seiten sind
 , ,
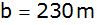 , ,
 lang. Von der Mitte der längsten Seite aus wird ein Weg zur
gegenüberliegenden Ecke angelegt.
lang. Von der Mitte der längsten Seite aus wird ein Weg zur
gegenüberliegenden Ecke angelegt. |
|
Berechne die Fläche F des Siedlungsgeländes. |
|
2 P |
|
|
Aufgabe 37a: |
Eine Eisenbahnstrecke ist geplant. Sie soll in geradem
Verlauf von Punkt A nach Punkt B (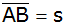 )
geführt werden. Ein Teil der Strecke wird als Tunnel gebaut.
Die Punkte A und B werden von einem dritten Punkt C aus wie
folgt vermessen: )
geführt werden. Ein Teil der Strecke wird als Tunnel gebaut.
Die Punkte A und B werden von einem dritten Punkt C aus wie
folgt vermessen:
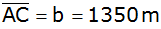 , ,
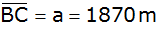 , ,
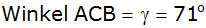 . . |
Wie lang (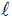 )
wird der Tunnel, wenn sein Eingangspunkt D von A die
Entfernung )
wird der Tunnel, wenn sein Eingangspunkt D von A die
Entfernung
 ,
sein Ausgangspunkt E von B die Entfernung ,
sein Ausgangspunkt E von B die Entfernung
 hat?
hat? |
|
2 P |
|
|
Aufgabe 37b: |
Eine Eisenbahnstrecke ist geplant. Sie soll in geradem
Verlauf von Punkt A nach Punkt B (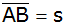 )
geführt werden. Ein Teil der Strecke wird als Tunnel gebaut.
Die Punkte A und B werden von einem dritten Punkt C aus wie
folgt vermessen: )
geführt werden. Ein Teil der Strecke wird als Tunnel gebaut.
Die Punkte A und B werden von einem dritten Punkt C aus wie
folgt vermessen:
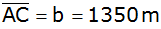 , ,
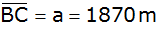 , ,
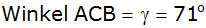 . . |
Wie groß sind die Winkel CAB ( )
und CBA ( )
und CBA (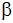 )? )? |
|
2 P |
|